理论分解框架与策略定义 [page::2][page::3][page::4]

• 时间序列动量策略根据单一资产过去k期收益确定权重，横截面动量以各资产相对收益偏差为权重。

- 时间序列动量期望收益分为自相关（Auto）、均值（Mean）两部分，横截面动量新增交叉相关（Cross）项反映品种间跨期收益协方差。

• 波动率拖累调整考虑了年化计算中的过高预期收益修正，是收益风险比分解关键因素。

实证回测验证分解公式准确性 [page::8][page::9]

• 时间序列动量策略在不同k回看期下，分解公式与实际回测收益风险比高度吻合。

• 年化收益风险比分解显示均值项长期稳定贡献正向，波动率拖累负影响明显，自相关项对收益贡献存在波动，峰值出现在k≈20左右。

• 横截面动量策略同样验证分解公式，呈现出与时间序列类似但多出交叉相关项的表现特征。

• 交叉相关项主要为负值，拖累横截面动量表现，表明资产间跨期负相关性降低策略表现预期。

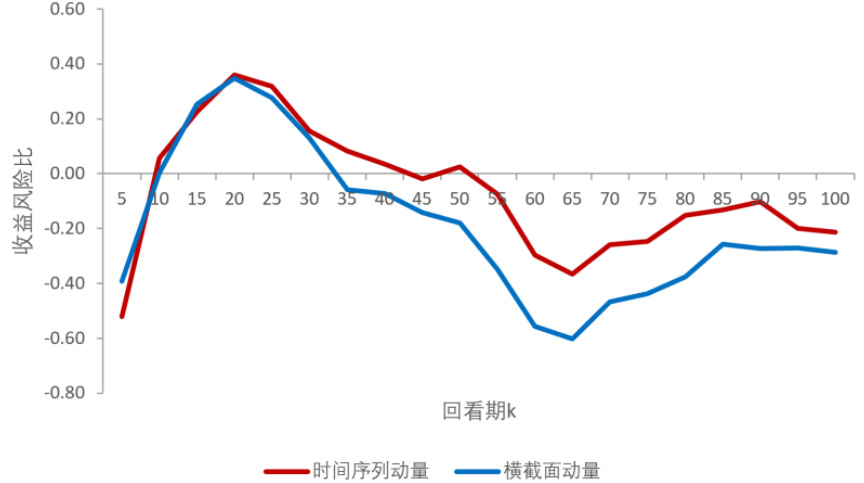
• 两种动量策略收益风险比对比显示，k较小时差异不大，k>20时时间序列动量明显优于横截面动量。

量化模型及策略应用启示 [page::0][page::10]

• 时序动量策略收益主要源于自相关和均值贡献，适合挖掘单品种趋势持续性。

- 横截面动量策略受品种间复杂协方差影响，交叉相关项为其特有收益调节因子，策略优化需关注资产跨期相关结构。

• 实证确认波动率拖累为负贡献，提示风险管理在动量策略设计中重要性。

- 回看期k选择为策略表现关键参数，经验值约为20期间效果最佳。

• 策略适用范围包括主力期货合约，具备自动分解校验方法，有助于策略调优和风险监控。

金融研究报告详尽分析报告

---

1. 元数据与概览

• 报告标题：《CTA 策略系列报告之十：时间序列动量还是横截面动量?》

- 分析师：于明明

• 研究助理：宫民

- 发布机构：兴业证券经济与金融研究院

• 日期：2019年08月14日

- 主题：研究并比较CTA（Commodity Trading Advisor，商品交易顾问）策略中两类主要动量策略——时间序列动量与横截面动量的期望收益风险比分解与收益来源机制。

核心论点简述：

该报告旨在理论推导与实证分析两种动量策略——时间序列动量（TSMOM）与横截面动量（CSMOM）——的期望收益风险比分解，从而深刻揭示动量因子的内在构造及其收益来源差异。通过将年化期望收益比拆分为自相关项、均值项、波动率拖累项（以及横截面动量中特有的交叉相关项），作者不仅明晰两种策略的收益生成机制，还以实证回测验证了理论公式的适用性。报告结论指向两种动量策略在不同市场环境及参数设置下表现的差异性，尤其交叉相关项对横截面动量策略收益有负向拖累作用。

---

2. 逐节深度解读

2.1 动量策略定义

2.1.1 时间序列动量策略定义（TSMOM）

• 定义：利用N个期货品种，基于各品种过去k期收益率大小赋权，构建权重为 $w{t}^{TS,i} = r{t-k,t}^i$。

- 组合收益： 组合下期收益率为各品种过去k期收益与未来一期收益的加权和：

$$
r{t,t+1}^{TS} = \sum{i=1}^N r{t-k,t}^i \cdot r{t,t+1}^i
$$

• 逻辑理解：利用单个品种的历史表现预测其未来走向，是一种“时间序列”上基于自我历史数据的趋势追踪方法。

2.1.2 横截面动量策略定义（CSMOM）

• 定义：基于N个期货品种最近k期收益率与全品种均值的差值赋予权重：

$$
wt^{CS,i} = r{t-k,t}^i - r{t-k,t}^{EW}
$$

其中均值权重为：

$$
r{t-k,t}^{EW} = \frac{1}{N} \sum{i=1}^N r{t-k,t}^i
$$

• 组合收益：

$$
r{t,t+1}^{CS} = \sum{i=1}^N (r{t-k,t}^i - r{t-k,t}^{EW}) r{t,t+1}^i
$$

• 逻辑理解：通过比较同一时点不同资产的表现，选择表现相对好的资产持有，较差的卖出，是跨资产横截面比较的动量效应。

---

2.2 动量策略收益风险比分解

2.2.1 时间序列动量策略期望收益分解及波动率计算

• 期望收益推导基础假设：

- 预期收益率 $\mu^i$ 对时间t不变；
- 将收益率向量及对应跨期协方差矩阵定义为：

$$
\mu = [\mu^1, \ldots \mu^N]^T, \quad
\Omega = E \left[(R{t-k,t} - k\mu)(R{t,t+1} - \mu)^T \right]
$$

• 期望收益率拆解：

$$
E(r{t,t+1}^{TS}) = tr(\Omega) + k \mu^T \mu
$$

其中：

- $tr(\Omega)$ 是自相关项，反映各品种收益率自协方差的贡献；
- $k \mu^T \mu$ 是均值项，由各品种收益均值平方和决定。

• 收益方差计算：

利用定义的方差-协方差矩阵 $\Omegak^A$，期望收益方差具体表示为所有品种收益率的方差和协方差的加权组合。

• 对策略波动率计算：

期望收益的标准差为该组合收益方差的平方根即波动率。

2.2.2 横截面动量策略期望收益分解及波动率计算

• 期望收益推导步骤：

横截面策略期望收益率为时间序列动量期望收益率减去均值权重对应组合的期望收益：

$$
E(r{t,t+1}^{CS}) = E \left(\sumi r{t-k,t}^i r{t,t+1}^i \right) - N \cdot E \left( r{t-k,t}^{EW} r{t,t+1}^{EW} \right)
$$

• 进一步推导，拆解为三项：

$$
E(r{t,t+1}^{CS}) = Auto^{CS} + Cross^{CS} + Mean^{CS}
$$

- 自相关项 ($Auto^{CS}$): 类似TS策略，由个别品种自协方差决定；
- 交叉相关项 ($Cross^{CS}$): 独有项，由品种间收益率跨期协方差决定。若不同时期两个不同品种收益率呈负相关，则该项贡献正向收益；
- 均值项 ($Mean^{CS}$): 由各品种收益率均值的方差贡献，反映收益差异性越大带来的潜在收益越高。

• 收益方差：

利用横截面收益定义，表达为时间序列收益方差与均值组合收益方差的差异，含有协方差调整项。

2.2.3 年化收益风险比分解及波动率拖累调整

• 目标：

将日度期望收益风险比（Sharpe比率）转化为年化版本，避免简单乘数方法带来的高估。

• 调整公式表达：

$$
Sharpe{year}^{TS} = \frac{(\mud^{TS} - 0.5 \sigmad^{TS2}) \times 250}{\sigmad^{TS} \times \sqrt{250}} = \frac{\mud^{TS}}{\sigmad^{TS}} \sqrt{250} - 0.5 \sigmad^{TS} \sqrt{250}
$$

同理，横截面动量策略类似处理。

• 重要性：

其中 $0.5 \sigmad^2$ 项体现了波动率拖累效应（Volatility Drag），即日度波动率越大，对年化收益的侵蚀越显著。

---

2.3 分解公式的验证与应用

2.3.1 数据范围及回测假设

• 数据: 选取28个流动性较好，上市时间充分的国内期货主力合约，样本时间2015.01.05至2019.06.26的复权价格走势。

- 调仓与成本: 每日调仓，不考虑交易成本，假设期货合约无限可分。

2.3.2 实际回测与分解公式比较

• 时间序列动量策略：

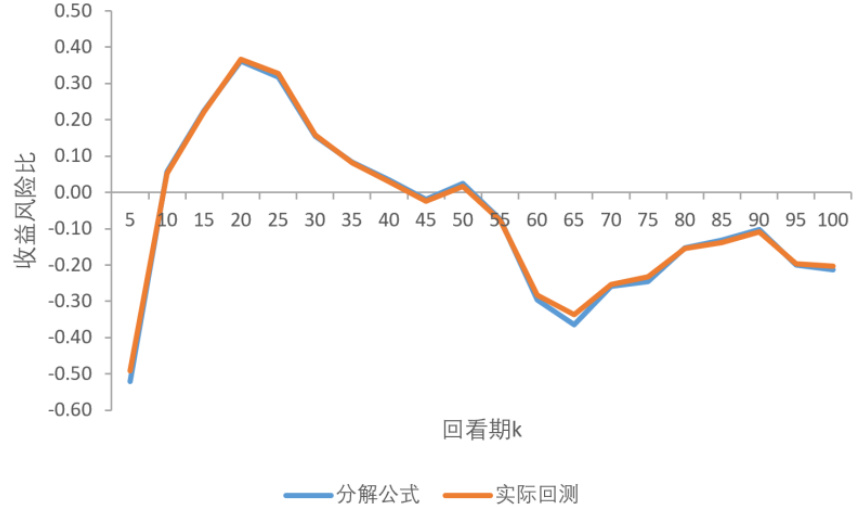
- 图1展示不同回看期k的年化收益风险比对比，分解公式与实测回测曲线高度吻合，说明理论模型有效。
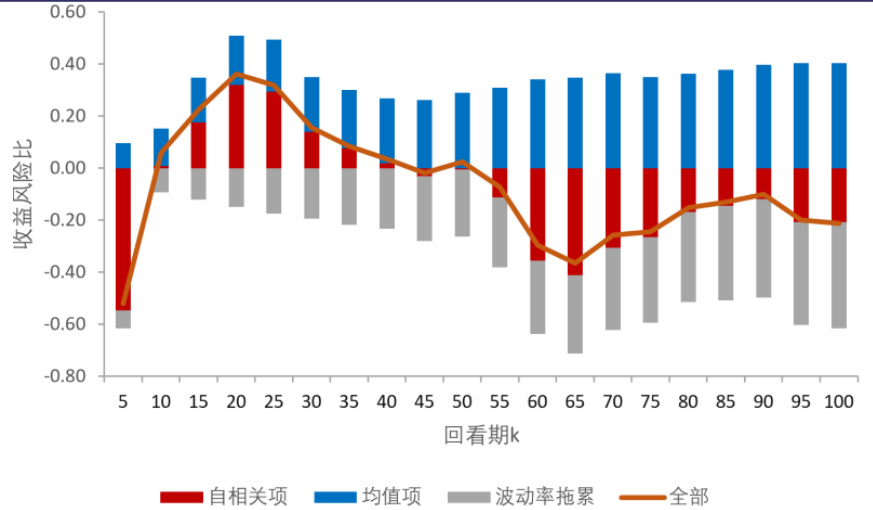
- 图2对收益风险比进行具体分解，均值项呈持续正向贡献，波动率拖累持续负向拖累，自相关项贡献随k变化，在k约20时表现最好。

• 横截面动量策略：

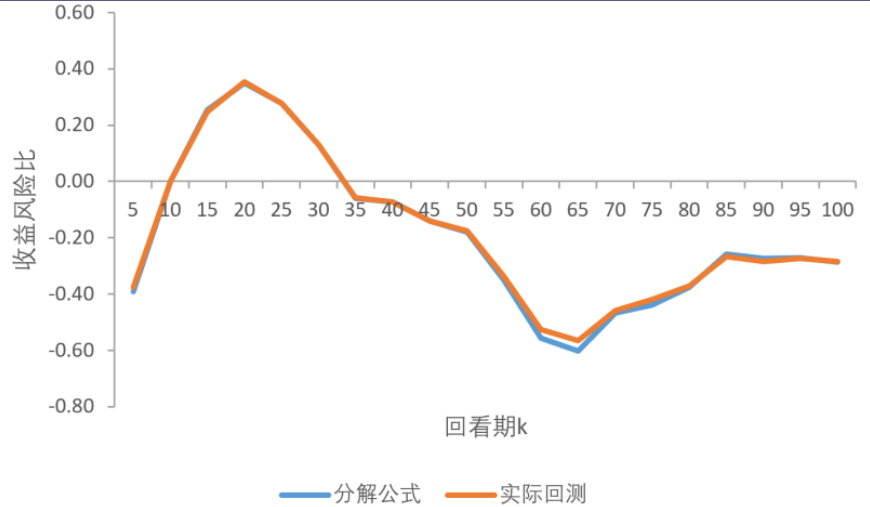
- 图3展示该策略收益风险比的分解公式与实测回测高度一致，验证方法准确。
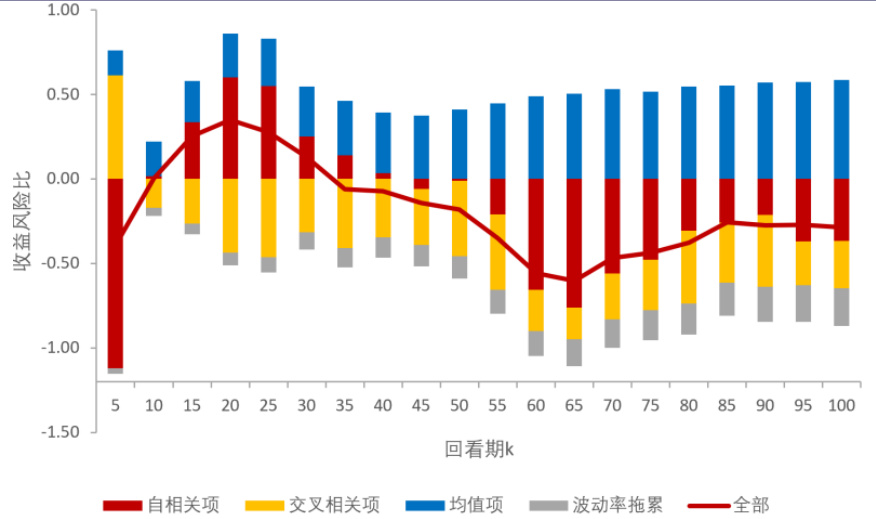
- 图4细分四项贡献：均值项正贡献，波动率拖累负贡献，自相关项贡献随k变化，且交叉相关项大多负贡献，仅在k=5时为正，显示交叉相关项对策略表现形成稳定拖累。
- 图5在小回看期k时，两种策略表现接近，k>20时时间序列动量明显优于横截面动量。

---

3. 图表深度解读

图1：时间序列动量策略期望收益风险比比较（第8页）

• 描述：展示时间序列动量策略在不同回看期k条件下，分解公式计算与实际回测得到的收益风险比对比。

- 解读：两条曲线紧密重合，说明理论公式在实际市场数据下能准确预测策略风险收益情况。其中k在10至30区间收益风险比较高，约0.3至0.4。

• 联系文本：验证了报告核心推导的有效性，强调分解享有稳定预测能力。

图2：时间序列动量策略期望收益风险比分解（第8页）

• 描述：按不同k，将收益风险比拆解为3部分：自相关项（红）、均值项（蓝）、波动率拖累（灰），总和用橙色线表示。

- 解读：均值项持续正收益。波动率拖累始终负收益且幅度较大。自相关项之于k=20左右贡献最大且为正。整体收益风险比趋势由三因素叠加决定，k越大波动率拖累越明显拉低表现。

• 联系文本：显示不同因素对收益贡献不同，允许策略优化聚焦提升自相关和均值贡献及控制波动率。

图3：横截面动量策略期望收益风险比比较（第9页）

• 描述：横截面动量策略在不同k条件下实际回测与分解公式的收益风险比比较。

- 解读：两者基本吻合，但整体收益风险比明显低于时间序列动量策略，表现较弱且更早进入负区间至k约30。

• 联系文本：通过验证模型准确，指出横截面策略整体表现略逊，并提示需关注影响因素。

图4：横截面动量策略期望收益风险比分解（第9页）

• 描述：对横截面策略收益风险比进行四项拆解：自相关项（红）、交叉相关项（橙）、均值项（蓝）、波动率拖累（灰），总和以红色线展示。

- 解读：均值项持续正向贡献，波动率拖累负向明显，交叉相关项多数情况下为负，体现资产间跨期协方差对策略性能的拖累。仅k=5时交叉相关项为正，显示短期存在改善空间。自相关项贡献随k波动。

• 联系文本：凸显横截面策略独特的交叉相关负贡献特征，构成该策略表现劣势的主因。

图5：时间序列与横截面动量策略期望收益风险比的比较（第10页）

• 描述：同图1和3对比两类策略年化收益风险比，红色为时间序列动量，蓝色为横截面动量。

- 解读：两者在小回看期k（5-20）时接近，但k超过20后，时间序列动量显著优于横截面，差距扩展，提示长期回看周期内TS策略更具有效收益风险比优势。

• 联系文本：汇总比较两策略优势时段及展现持续性表现差异。

---

4. 估值分析

本报告不涉及直接的典型估值分析（如DCF、P/E等），而是重点在策略的收益风险比分析与理论分解。若要将该报告视作对动量因子投资价值的“估值”，其方法可视为对预期收益风险比的分解和理解，侧重从信号来源及统计特性视角“定性定量”评估策略表现。

年化期望收益风险比的拆分及波动率拖累的考虑，等价于对风险调整回报的更精准模型估计，从而提升策略运行效果的评估准确性。这种方法论属于因子投资和量化策略评估的重要范畴。

---

5. 风险因素评估

• 市场环境变化风险：报告明确提示所有结论基于历史数据，在市场环境转变时模型存在失效风险，特别是动量效应可能减弱或逆转，导致策略失效。
• 策略参数敏感性风险：自相关项对收益风险比的贡献依赖回看期k的选择，若回看期设定不合理，可能导致策略表现波动性加大。
• 交叉相关项风险：横截面动量策略的交叉相关项多数为负，表明品种间跨期收益的高度正相关性导致潜在收益被拖累，若未来相关结构变化，可能使策略表现更差。
• 交易成本及市场流动性风险：报告默认无交易成本和无限可分，无限流动性假设，现实交易中可能由于滑点、手续费等大幅影响策略表现。
• 数据及模型假设风险：收益率期望和协方差矩阵假设时间稳定且准确估计，实际中模型估计误差及非稳定性可能降低策略执行效果。

报告未详细给出具体缓解策略，提示用户须结合市场实际灵活调节。

---

6. 批判性视角与细微差别

• 报告在动量策略期望收益和风险的分解中，假设收益率的期望和协方差矩阵是常数且稳定，这可能在市场剧烈波动或结构性变化时失效，影响模型的实用性。
• 波动率拖累项被重点强调，且为收益风险比的负面贡献者，但报告未具体展开如何通过组合优化或风险管理技巧降低波动率影响，留有进一步研究空间。
• 横截面动量策略中交叉相关项的持续负贡献指示若能选取相关性更低品种组合，则效果可提升，报告未详述如何构建或识别这种组合，是未来可拓展点。
• 实证部分采用的28个品种主要是国内期货品种，数据覆盖时间相对有限（约4.5年），不排除特定市场结构的偏倚导致结果在其他市场或更长周期的不同表现。
• 交易成本假设为零，与现实差异较大，实际应用时策略净收益需剔除成本影响，整体收益风险比可能下降。
• 报告用词严谨，未明显偏向，结论建立在理论推导与实证验证的严格匹配，展现较强的学术深度与实际指导意义。

---

7. 结论性综合

本文从理论与实证两个维度系统分析了CTA策略中两类主流动量策略——时间序列动量与横截面动量的期望收益风险比分解。核心贡献在于：

• 理论推导上，对两种策略的日度及年化期望收益率与波动率进行了数学拆解，揭示其内生的收益来源：

- 时间序列动量策略收益分解为自相关项（由品种自身跨期协方差决定）、均值项（收益率均值平方和）及波动率拖累项（波动率平方下降年化收益）；
- 横截面动量策略在此基础上进一步包含交叉相关项，反映不同品种间的跨期协方差影响。

• 实证测试上，通过对28个国内主流期货品种近4.5年的复权价格数据回测验证了分解公式的有效性，主要发现：

- 各因素对收益风险比贡献稳定，尤其均值项对两种策略均为正贡献，波动率拖累为负贡献；
- 自相关项贡献随回看期k调整，k约20时收益风险比水平达到峰值；
- 交叉相关项普遍对横截面动量策略造成负向拖累；
- 综观表现，时间序列动量策略整体优于横截面动量策略，尤其是中长期回看期。

• 策略应用及启示：

- 动量策略设计时，需关注回看期参数选择；
- 控制波动率拖累是提升年化收益风险比关键；
- 横截面策略受制品种间跨期相关性约束，如能优化品种选择，可能提高表现；
- 理论与数据验证的一致性，为CTA策略设计提供坚实的理论基础与实践指导。

• 风险提示：

报告反复强调模型基于历史数据，有市场环境切换风险；实际交易应考虑交易成本及流动性限制。

综上，报告系统而深入地揭示了两种动量策略的经济学与统计学本质，辅以实证检验，具有较高的理论研究价值及实际指导意义，建议投资者和策略设计者关注自相关、均值和交叉相关因子对收益的影响，以及波动率拖累的管理，优化动量策略的回看期和资产组合，从而更好地实现收益风险平衡。

---

参考图表（均来源于报告，点击查看原图）

• 

图1：时间序列动量策略期望收益风险比比较

• 

图2：时间序列动量策略期望收益风险比分解

• 

图3：横截面动量策略期望收益风险比比较

• 

图4：横截面动量策略期望收益风险比分解

• 

图5：时间序列与横截面动量策略期望收益风险比的比较

---

全文引用页码标记：[page::0,1,2,3,4,5,6,7,8,9,10]

结束语

本报告分章节清晰构建了动量策略理论与实证分析框架，提供了对CTA策略设计及风险评估的深刻洞察，值得量化投资者、策略研究员及风控人员认真研读、参考和借鉴。

报告