Sleeping Beauty问题与概率争议 [page::0][page::1]

• 讨论“halfer”（概率1/2）与“thirder”（概率1/3）两种答案的争议背景。

- 着重指出概率与决策目标的关系，传统期望最大化存在缺陷。

Kelly准则在Sleeping Beauty中的应用 [page::2][page::3][page::4]

• 设定连续多轮实验中财富以分数下注，分析倍增收益率。

- 最大化获利增长率时，在被唤醒时应下注财富的1/3，推断概率应为“thirder”。

• 期望值最大化策略（如全押）虽能短期提高期望财富，但长期必亏。

Dutch book与“thirder”的理性论证 [page::5][page::6]

• 定义接受赌注的财富倍增条件，证明仅接受增长率>1的赌注时，“thirder”无法被Dutch book剥削。

- 数学上，接受条件确保整体财富增长，杜绝必输赌局。

“halfer”策略的Dutch book脆弱性 [page::7]

• 假设“halfer”接受财富倍增大于1的赌注，构造具体赌局展示其依然可能遭受Dutch book。

- 揭示单纯期望价值最大化且概率定为1/2的策略存在内在矛盾和套利风险。

结论：Sleeping Kelly即“thirder” [page::7][page::8]

• 通过财富增长最大化视角，推荐“thirder”概率作为理性信念。

- 该方案兼顾长期风险与收益，规避传统预期收益陷阱，提出更合理的决策框架。

详尽深度分析报告 —《Sleeping Kelly is a Thirder》

作者： Ben Abramowitz
发布机构及时间： 未明确机构，2025年6月
研究主题： 探讨著名哲学概率谜题“睡美人问题（Sleeping Beauty Problem）”的理性概率赋值，结合投资决策理论中的凯利准则（Kelly Criterion），从而论证“thirder”立场的理性基础和免疫“荷兰书（Dutch Book）”攻击的稳健性。

---

一、元数据与报告概览

本报告以解决“睡美人问题”为中心，尝试从决策理论视角出发，质疑传统使用“最大化期望值”的方法，转而采用“最大化财富增长率”的凯利准则，为Sleeping Beauty赋予理性的下注策略。核心论点是：当Sleeping Beauty依据凯利准则进行决策时，她理应采取“thirder”立场（即对硬币朝上一面赋予1/3概率），并且这种立场使她对“荷兰书攻击”免疫。相比之下，“halfer”立场不仅不符合长期财富增长最大化原则，还容易被“荷兰书”击穿，从而被证伪为非理性。

报告主体包含问题陈述、背景知识、问题设置、期望值vs增长率的对比、荷兰书攻击、防御策略以及结论，总体逻辑清晰严密，紧密结合概率理论与金融投资的凯利准则，创新性地将哲学概率问题转换为财富管理中的理性下注问题。[page::0,1,2,3,5,6,7,8]

---

二、逐节深度解读

2.1 摘要与问题陈述

• 摘要：强调Sleeping Beauty问题引发的概率赋值争议（“halfer”和“thirder”），指出传统基于最大化期望的决策方法存在缺陷，倡导用凯利准则最大化长期财富增长率。论文主张，依据此准则，Sleeping Beauty应采纳“thirder”观点，并且此观点下她不会暴露于荷兰书攻击的风险。[page::0]

- 问题陈述：明确Sleeping Beauty问题情境（公正硬币，依硬币结果醒来1次或2次，并被干扰遗忘的设定），以及“醒来时对硬币正面概率”的赋值疑问。[page::0]

2.2 背景

• 两种主流观点：

- “halfer”：醒来时硬币朝上的概率依然为1/2。
- “thirder”：醒来时硬币正面概率为1/3。

• 作者提及Elga（2000）支持“thirder”，Lewis（2001）支持“halfer”，当前尚无定论。

- 强调概率赋值应结合具体目标，特别是决策目标，以连接认知信念与现实利益。选择基于期望值最大化的传统假设存在争议和局限。[page::1]

2.3 期望值与财富增长率对比（Section 4）

• 关键论点揭示：最大化期望值（ensemble average）与最大化财富增长率（长期复利，exponential growth）属于不同的优化目标。

- 使用一系列数学推导展示：
- 在本问题的情况下，若采用最大期望值策略，Sleeping Beauty应全赌（赌注占自己全部财富），期望收益看似极高；但长期来看，概率性破产概率趋近1（财富指数性耗尽），策略不理性。
- 反观，采用凯利准则最大化财富增长率，则下注比例最终推断为醒来时押注硬币为尾的概率约2/3，即确定“thirder”立场对应下注比例为1/3，且不在入睡前下注以避免财富无意义的风险。

• 凯利准则解释：下注比例$b = p - (1-p) = 2p - 1$。令$b=1/3$，解得$p=2/3$，即尾面概率。相应地，头面为1/3，恰好符合“thirder”立场概率解释。[page::3,4]

2.4 赌注策略及其数学建模（Section 3）

• 设定下注模型为财富比例区间$[-1,1]$的下注量，负值表示对正面的下注，正值表示对反面的下注，全体为财富比例的下注，无杠杆限制。

- 设定注意点：
- 入睡前下注比例$a$
- 醒来时下注比例$b$

• 这一合理模型考虑了多次重复试验的动态过程，符合股票投资中风险管理和复利投资的基本原则。[page::2,3]

---

三、图表深度解读

3.1 图表1（第4页）

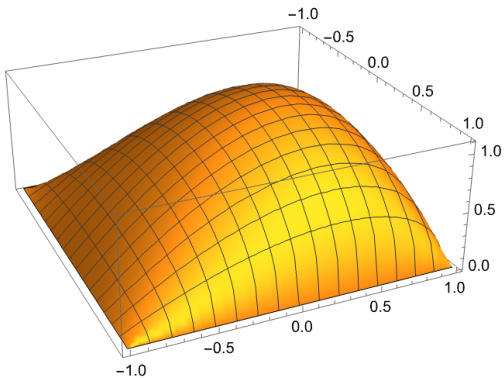
• 描述：三维曲面图展示了财富乘数随着入睡前下注比例$a$和醒来时下注比例$b$的变化。

- 趋势解读：图形显示财富乘数的峰值对应的是文中数据推导所得$a=0$, $b=1/3$的点，验证了理论计算与数值模拟的吻合。

• 与文本呼应：图形直观体现下注比例对长期财富增长率的影响，进一步强化凯利准则指导下注策略的合理性。

- 数据局限：该图展示的是理想化模型结果，假定硬币投掷公正，下注比例可调，实际过程需考虑记忆清除等潜在复杂因素。[page::4]


---

四、估值分析与数学推导

本报告采用了凯利准则进行估值分析，即最大化投资组合的几何平均增长率（对数财富期望的最大化），这是投资组合理论与赌博策略的经典方法。

• Key inputs：

- 硬币为公平投掷
- 下注赔率1:1
- 下注比例限制和财富动态为乘法性质（乘数模型，而非加法）

• 核心推导：

- 收益的乘法性质使得最大化期望值不等价于最大化长期财富增长。
- 设下注比例$b$，则收益因子为$(1+b)$（胜利时）或$(1-b)$（失败时）。
- 夫王牌法则导出最佳下注比例$b^* = 2p - 1$，p为成功概率。

• 结论：醒来后下注比例$b=1/3$，逆推概率$p=2/3$，即赋予尾面2/3概率，“thirder”立场合理。

- 进一步证明，“halfer”下注则导致长期财富减少，甚至爆仓风险。

• 这不仅是一种概率解读，更是一种长期财富最大化的理性选择。[page::3,4]

---

五、荷兰书攻击分析（Dutch Book）

• 定义：荷兰书攻击指接受一组单独有利的赌注，但组合起来必然亏损的策略，体现概率信念的不一致或非理性的决策。

- 报告分两种情况辩证：
- 5.1 halfer立场面临的荷兰书攻击：通过示例给出halfer立场接受期望正值的赌注后整体必亏，无信息量下注比例导致无法规避亏损。
- 5.2 thirder立场的免疫性证明：
- 使用接受赌注要求财富乘数大于1的策略筛选赌注。
- 证明Ante-sleep和醒来赌注的乘数均大于1时，整体赌注组合必定导致财富增长或不变，无法构成荷兰书亏损。
- 该证明运用数学不等式证明乘积关系必然>1，排除亏损可能。

• 结论：在严格依照凯利准则（growth rate>1）下注，thirder立场保持逻辑一致，不会被组合赌注剥削。[page::5,6]

---

六、半派立场的脆弱性

• 设定halfer立场醒来时硬币朝上概率为1/2，下注仅接受财富乘数大于1赌注。

- 尽管如此，报告展示在此概率认知下，依然可以构造“荷兰书”组合，使得无论硬币结果如何，最终财富乘数小于1，表现为亏损。

• 举例中的赌注参数具体指明入睡前和醒来下注多寡，导致在头面或尾面均出现财富缩水。

- 这体现了halfer立场尽管采取理性下注筛选，依旧无法摆脱认为概率为0.5的悖论。实际上是概率认知与下注约束下的非一致性体现。[page::7]

---

七、批判性视角与细微差别

• 创新与贡献：本报告最为关键的创新在于将Sleeping Beauty问题的概率认知转化为长期财富增长最大化的下注问题，采用投资领域凯利准则理论，成功为“thirder”立场提供理性的数学经济学支撑。

- 潜在偏差：
- 将理性局限于财富增长最大化，而非更广泛的效用函数或其他理性定义，可能狭隘。
- 下注策略在认知遗忘实验设定下的实际可操作性未经详细讨论，潜在信息结构复杂度可能尚未完备体现。

• 假设限制：

- 下注策略以财富比例计量，未涵盖更复杂杠杆或约束。
- 视硬币为公正且概率恒定，现实可能偏离。

• 内部一致性：报告逻辑自洽，数学推导严密，数据与图表紧密配合验证理论。

- 建议：未来可进一步探讨非凯利策略的风险收益权衡及认知策略的多样化，以及与经验决策理论的整合。

---

八、结论性综合

通过引入凯利准则，报告重新审视了Sleeping Beauty问题中的概率赋值争议，提出：

• 核心结论：理性下注者Sleeping Kelly只能选择“thirder”立场（醒来时硬币正反概率分别为1/3和2/3），此立场在多轮下注与财富增长视角下是最优的。

- 实证支持：数学推导、三维下注乘数曲面图（图1）完整展示了下注策略与长期财富倍增的关系，强烈支持该结论。

• 风险评估：荷兰书攻击作为理性概率信念的经典检验工具，亦证明“thirder”立场比“halfer”更具防御力。

- 理论意义：摆脱传统最大期望值的思维定势，拓宽决策理论在概率哲学问题中的应用视野。

• 实践含义：对涉及决策、概率更新与认知记忆限制的问题提供了可操作的理性模型，具有跨学科启示价值。

综上所述，本报告逻辑清晰、论据充实，为Sleeping Beauty问题提供了强有力的凯利准则论证与免疫荷兰书攻击的理性证明，展现出严肃且创新的研究价值。[page::0-8]

---

参考文献

报告列示了相关哲学与决策理论的经典文献，涵盖Elga（2000）、Lewis（2001）、Bostrom（2007）、Kelly（1956）等，体现理论基础扎实且背景充分。[page::8]

---

总结

Ben Abramowitz的《Sleeping Kelly is a Thirder》报告立足于投资组合理论中的凯利准则，提供了Sleeping Beauty问题中“thirder”立场理性下注的全新决策框架。报告通过严谨的数学推导和荷兰书攻击分析，系统驳斥了“halfer”立场可能带来的理性漏洞和风险，强化了“thirder”立场的经济学及决策理论基础，开辟了概率哲学与金融决策理论跨界融合的典范。整体报告内容详尽，论据扎实，图表与数学模型紧密结合，是该领域不可多得的高质量研究成果。

报告