1. 研究背景与目标 [page::1]

• 探讨LLMs在多智能体博弈环境中的战略推理能力，不同于以往对个体单决策推理的研究。

- 采用行为经济学中经典的p-Beauty Contest Game、猜测游戏和11-20金额请求游戏作为测评工具。

• 使用层级理性（level-k）模型和认知层次（cognitive hierarchy）模型量化LLMs的推理深度。

2. 评估方法与模型概要 [page::2][page::4][page::5]

• level-k模型假设参与者推理层级依次递增，player-k认为其他都是k-1级推理。

- CH模型假设参与者推理层级服从泊松分布，推理层级混合更为复杂。

• 利用最大似然估计（MLE）估计模型参数，分布描绘LLMs的战略推理层级分布。

3. p-Beauty Contest Game基线结果 [page::6][page::7][page::8]

• 推理型LLM（如GPT-o1、Claude-3.5、Gemini-2.0）平均推理层级显著高于标准LLM。

- GPT-o1表现最佳，呈现更多高阶战略推理行为（如$L_{\infty}$）。

• 在不同参数条件下推理型LLM保持优越性，标准LLM表现波动且落后于人类。

4. p-Beauty Contest Game多轮学习实验 [page::9][page::10]

• 所有LLM均能通过反馈调整行为，表现出策略迭代和学习的能力。

- 推理型LLM收敛速度远快于标准LLM，且初始响应更接近理性均衡预测。

• GPT-o1持续领先，表现出接近人类甚至超越人类的学习和推理效率。

5. 猜测游戏与11-20金额请求游戏表现 [page::12][page::13][page::16]

• 猜测游戏中，推理型LLM GPT-o1和Gemini-2.0呈现明显高阶战略推理，超过人类平均水平。

- 11-20金额请求游戏中，Gemini-2.0和GPT-o1表现突出，部分标准LLM表现较弱。

• 总体来看，多数推理型LLM具备较强的高阶策略思考能力，标准LLM能力有限。

6. 推理能力差异及机制解释 [page::16][page::17]

• 推理型LLM采用链式思维（chain-of-thought）和大规模强化学习训练，能分步细化问题、反复审视策略。

- 标准LLM虽具备基本规则理解，但在复杂多轮战略交互中表现欠佳。

• 多轮交互反馈机制对提升LLM的战略推理能力至关重要，为未来Agentic AI和AGI的发展提供借鉴。

The Emergence of Strategic Reasoning of Large Language Models: 深度详尽分析报告解构

---

1. 元数据与概览

• 报告标题：The Emergence of Strategic Reasoning of Large Language Models

- 作者：Dongwoo Lee、Gavin Kader

• 发布时间：2025年2月10日

- 研究主题：检验大型语言模型（LLMs）在多智能体战略环境中的战略推理能力，通过多个博弈论经典游戏测试标准LLMs与专门的推理型LLMs的表现差异，及其与人类水平的比较。

• 核心论点：

- 标准LLMs虽具备一定的个体推理能力（如编程、数学）但缺乏战略推理实力。
- 专门设计进行推理训练的LLMs表现出显著更高的战略推理层次，部分甚至超过人类水准。
- 战略推理能力的提升与模型使用的多步思考（chain-of-thought reasoning）、大规模强化学习等技术密切相关。
- 本研究通过行为经济学的层级理性模型（level-k模型、认知层级模型CH）定量评估LLMs的战略推理深度，揭示推理机制在实现更逼近人工智能的智能战略决策中的关键作用。

[page::0] [page::1]

---

2. 逐节深度解读

2.1 引言部分

• 论点总结：强调LLMs已在纯个体决策问题中展现强大推理技能，但是否能“预测他人行为并调整自身策略”的多智能体战略推理尚未被充分验证。

- 方法论：
- 选用行为经济学中著名的3个博弈（一维beauty contest、猜猜看游戏、11-20叫价游戏），这些游戏规则简洁、策略空间清晰，非常适合评估有限理性和递归推理。
- 采用层级理性模型（level-k模型）和认知层级模型（CH模型），两者都基于“参与者认为其他人低一层推理”的假设，但CH模型允许推理层级为混合分布（Poisson分布）。

• LLM选择与分类：包括3款标准LLMs（ChatGPT-4, Claude-2.1, Gemini 1.5）以及3款经过增强推理训练的LLMs（GPT-o1, Claude-3.5-Sonnet, Gemini Flash Thinking 2.0）。

- 评估方式：每个游戏LLM重复独立运行100次，模拟实验室100名独立参与者的决策数据，用MLE（最大似然估计）拟合层级理性模型参数。

2.2 层级理性模型与认知层级模型说明

• 层级理性模型（level-k model）设定：

- Rank-0玩家毫无策略意识、随机选择。
- Rank-1玩家假设所有对手为Rank-0。
- 递归类推，Rank-k玩家假设所有对手为Rank-(k-1)。

• 认知层级模型（CH）设定：

- 玩家假设对手混合分布于比自己低的推理层级，比例符合Poisson分布参数τ。

• 两种模型均用于测定LLMs的“战略推理深度”及预测其行动分布。

2.3 对比战略推理能力与训练机制

• 推理增强型LLMs（GPT-o1、Ge-2T、Cl-3S）体现更高战略推理等级，且收敛速度快。

- 这种能力差异可能源于它们采用了大规模强化学习、chain-of-thought（多步逐层思考）推理机制，模拟了人类推理逐步拆解复杂问题的方式，使其能不断修正策略，反复反思。

• 标准LLMs则大多表现为低层级推理行为，策略前瞻性弱，难以有效预测、调整应对他人行为。

[page::1] [page::2]

---

2.4 p-Beauty Contest Game（pBCG）章节详解

游戏描述

• 多个玩家（n≥2）在0-100区间选择数字，赢家是选中值最接近$p$倍全体选择均值的玩家。

- $p<1$时纳什均衡：所有玩家选0；$p>1$时纳什均衡：所有玩家选100。

理论模型

• Level-k模型最佳猜测序列：

$$l0=50, l1=50p, l2=50p^2, \ldots, lk = 50 p^k$$
当k趋于∞，若$p<1$则趋向0，若$p>1$则趋向100。

• CH模型基于Poisson分布$ fk(j;\tau) $加权，最佳猜测：

$$sk = \sum{j=0}^{k-1} fk(j;\tau) sj$$

• 采用最大似然估计拟合模型参数，估计LLMs出手的概率分布，对应各层次推理比例。

设计与实验

• 基线参数：$p=2/3, n=11$，每个LLM完成100次独立实验作答。

- 变体包括不同$p$值（1/2, 4/3），不同参与数$n$，目标统计量计算以均值或中位数等，模拟不同游戏环境。

• 还有10轮反馈重复游戏版本，探索LLM的学习与适应能力。

结果分析

• 图1（六个子图）展现不同模型与条件下不同LLM在level-k模型中的行为频率分布。

- 颜色代表不同LLM：橙色为GPT-o1，绿色为Gemini-2T Flash Thinking等。
- GPT-o1整体明显向更高层级（$L2$, $L{\infty}$）偏移，表现最强。
- 标准LLMs多集中于$L0$, $L1$，表现较弱。
- 不同参数条件下，大部分LLMs表现持平或略有降低，惟GPT-o1和Ge-2T在部分条件仍保持较高推理层次。
- 4/3的$p$值条件下，多数LLMs表现退化，可能因训练数据偏向$p<1$的版本，体现训练适应性局限。

• 表1展示CH模型参数$\tau$估计，反映推理步数的平均水平：

- GPT-o1在基线条件$\tau=4.42$遥遥领先，暗示超过大多数人类实验数据的约2倍推理深度。
- GPT-4、Cl-3S、Ge-2T表现优异但略低于GPT-o1。
- 标准LLMs Cl-2 和 Ge-1 平均推理层次数较低，接近或低于人类基准。

• 多轮反馈游戏中（图2），所有LLMs均表现出一定的学习适应能力：

- GPT-o1表现最优，初始即接近理性预测，随后快速调节逼近纳什均衡（$L{\infty}$）。
- 其他LLMs表现则存在较大差异，标准LLMs普遍推理层级较低，但多年反馈下也能提升。
- LLMs学习曲线与既有实验中的人类表现类似，说明在带有反馈的战略环境，LLMs能逐步提升推理复杂度。

[page::3] [page::4] [page::5] [page::6] [page::7] [page::8] [page::9] [page::10]

---

2.5 Guessing Game（GG）章节详解

游戏描述

• 两名玩家分别猜测对方的猜测，目标为尽可能接近对手猜测乘以各自的目标比例$p^i$，并且猜测值有限定区间。

- 两玩家目标不对称，导致独特的纳什均衡预测。

• 该游戏因有限回合的显性消除策略可被称为“优势可消除”（dominance-solvability）游戏。

理论侧重

• Level-k模型与CH模型在该游戏中预测同样遵循递归结构，同时结合玩家各自的范围限制，精确计算不同推理层的最佳响应。

实验设计

• 16个不同参数组合的游戏（注重$p^i$、上下界，详见表A6）。

- LLM持续进行16轮猜测，记录响应序列。

• 鉴于标准LLMs未能持续给出正确最佳响应，数据分析主要聚焦三款推理LLMs。

结果分析

• 图3的level-k分布显示：

- Cl-3S大多数响应停留在$L0$和$L1$水平。
- Ge-2T部分响应达到更高层次，表现与人类实验数据接近。
- GPT-o1频率最高的类别是$L{\infty}$，超越人类水平。

• CH模型的$\tau$估计（见表2）佐证该点，GPT-o1比其他模型和人类多2步推理。

- 在16轮轮次的个别比较中，GPT-o1在12轮中均展示出更强战略推理能力。

[page::10] [page::11] [page::12] [page::13] [page::14] [page::15]

---

2.6 Money Request Game（MRG）章节详解

游戏描述

• 两玩家选整数11-20，其金额对应数字大小。

- 若选数比对手少1，奖励20点额外奖金。

• 没有纯纳什均衡，体现更复杂的策略选择环境。

理论结构

• Level-k模型中：

$$l0=20, l1=19, l2=18..., l9=11$$，对应各层依次“抄底”对手行为的策略。

• CH模型基于Poisson分布权重加权层级猜测，取整数并减1。

结果解析

• 在该游戏中推理水平差距不如前两游戏明显。

- 图4显示：
- Ge-2T触及最高层级，Cl-2表现优于多数推理LLMs。
- GPT-o1表现优于多数，但Cl-3S几乎随机应答。
- 人类实验中多数为$L2$至$L_3$层级，高于LLMs平均水平。

• CH模型$\tau$估计（表3）与level-k吻合，LLMs整体推理步数低于人类（$\tau=3.14$）。
• MRG（Game 3）的小变体分析（附录B）说明某些LLM（GPT-o1、Cl-3S）对奖励结构变化较敏感，表现出轻微提高推理水平。

[page::13] [page::14] [page::15] [page::16] [page::17]

---

2.7 总结与论述

• 研究确认推理增强LLMs较标准LLMs在战略推理游戏中表现卓越，且多游戏跨环境表现稳健。

- 标准LLMs在一次性决策环境下推理严重受限，在重复博弈中可通过反馈提高推理水平但仍不及推理LLMs。

• 连续反复的任务反馈机制及chunk化推理极大增强LLMs推理深度和速度。

- 该研究支持了未来Agentic AI、AGI系统对高级战略推理能力的需求，推理能力是多智能体交互环境下决策执行的基石。

[page::16] [page::17]

---

3. 图表深度解读

3.1 图1 — pBCG中不同参数与LLMs的level-k分布

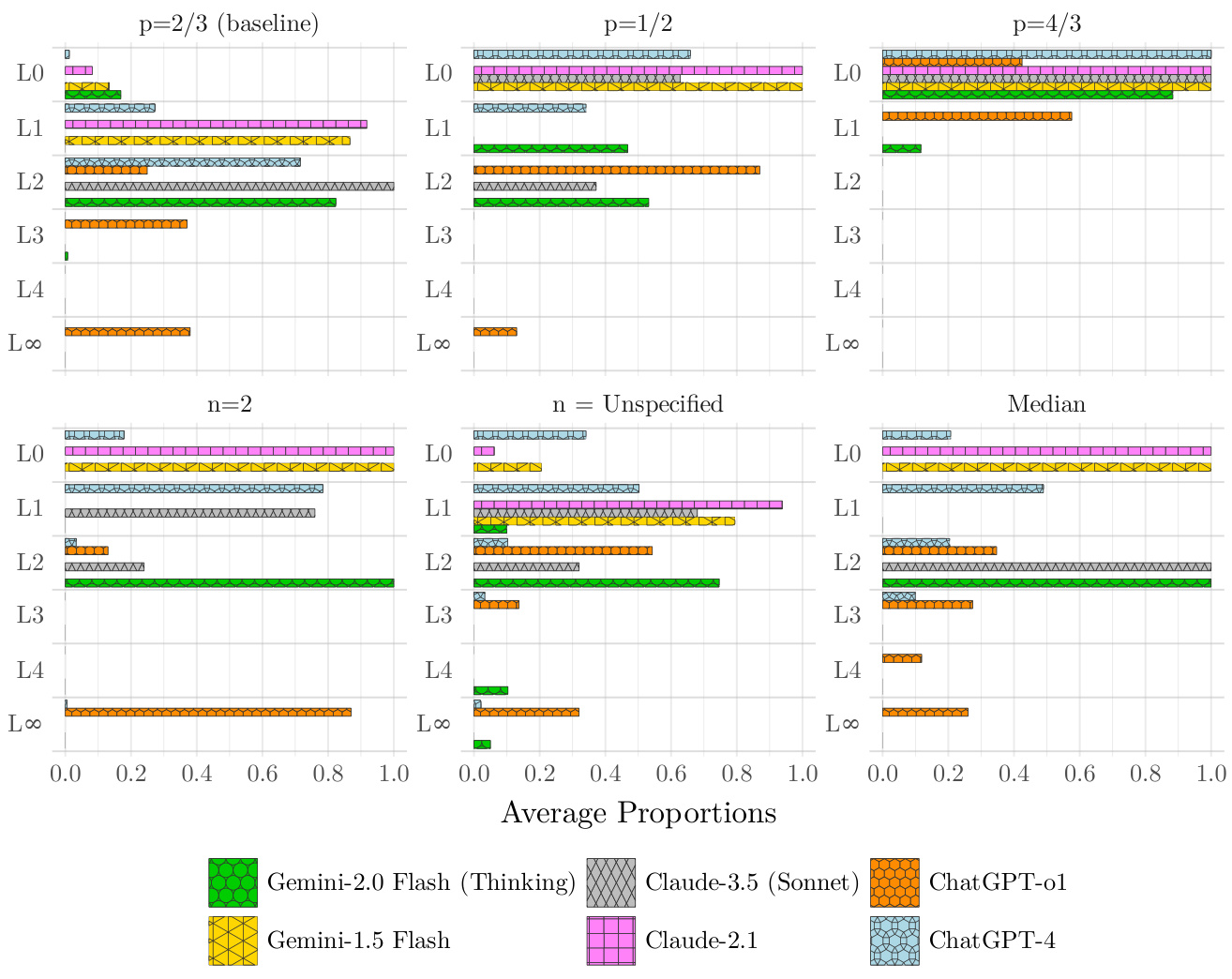
• 内容说明：展示六个游戏参数条件下，各LLM在level-k模型多个层级的平均响应比例。

- 数据解读：
- GPT-o1与其他推理LLMs（Cl-3S、Ge-2T）相比，在高层级（L3，L∞）上明显比率更高，标准LLMs多停留在L0-L1。
- $p=2/3$基线条件及$n=2$时GPT-o1表现尤其突出，接近理性（L∞）。
- $p=4/3$条件大部分模型表现下降，可能因训练数据偏向$p<1$。

• 支持文本论点：该图直观展现推理模型深度的差异，强化文本对推理LLMs优越性的论断。

3.2 表1 — CH模型τ参数估计（pBCG）

| LLM | p=2/3(baseline) | p=1/2 | p=4/3 | n=2 | n=unspecified | Median |
|---------|-----------------|--------|--------|--------|---------------|---------|
| GPT-4 | 2.39 (2.23,2.46)| 0.56 | 0.00 | 0.87 | 0.83 | 1.09 |
| GPT-o1 | 4.42 (4.00,4.77)| 2.52 | 0.95 | 7.09 | 3.43 | 4.00 |
| Cl-2 | 0.91 | 0.00 | 0.00 | 0.00 | 0.91 | 0.00 |
| Cl-3S | 2.87 | 1.50 | 0.00 | 1.17 | 1.26 | 2.87 |
| Ge-1 | 0.86 | 0.00 | 0.00 | 0.00 | 0.77 | 0.00 |
| Ge-2T | 2.46 | 2.12 | 0.00 | 1.86 | 2.22 | 2.46 |

• 解读：τ代表认知层级的平均值，越大代表平均战略推理层次越深。GPT-o1在所有条件尤其$n=2$显著领先，体现最高战略推理深度。

- 局限：p=4/3条件所有模型均显著退化，说明数据库偏向于$p<1$条件，影响模型学习和泛化。

3.3 图2 — 重复回合pBCG响应时间序列

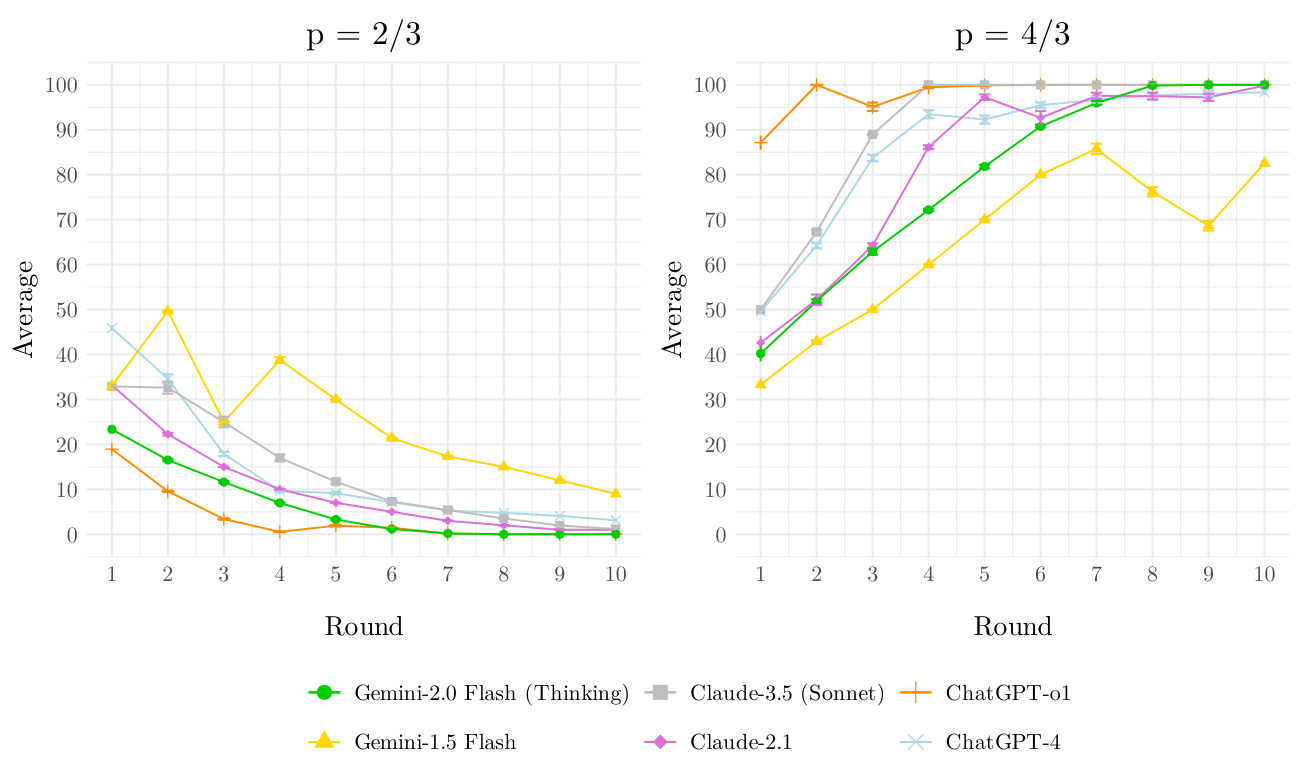
• 内容说明：显示p=2/3和p=4/3两种参数下，各LLM在10轮中平均响应值变化趋势。

- 解读：
- 对p=2/3，所有推理LLMs响应逐步趋于纳什均衡（趋向0），其中GPT-o1收敛最快。
- p=4/3条件下响应逐轮上升趋向100（纳什均衡），同样GPT-o1表现最佳。
- 反馈机制显著促进了LLMs的学习和适应能力，特别是推理型模型。

3.4 图3 — GG设定下level-k分布

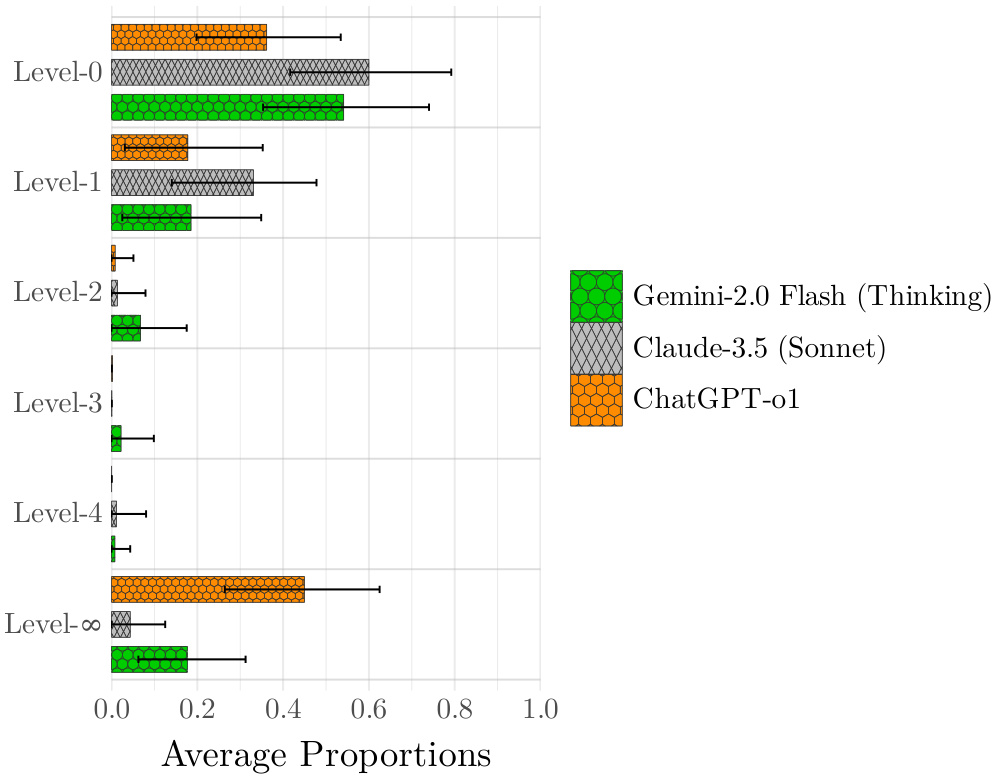
• 内容说明：GG的level-k行为分布估计，含95%置信区间，展现不同LLM的层级分布情况。

- 解读：GPT-o1高级推理占比最大（L∞），Cl-3S集中于L0-L1层，Ge-2T表现与人类相当，说明推理LLMs表现分化明显。

3.5 图4 — MRG设定下level-k分布

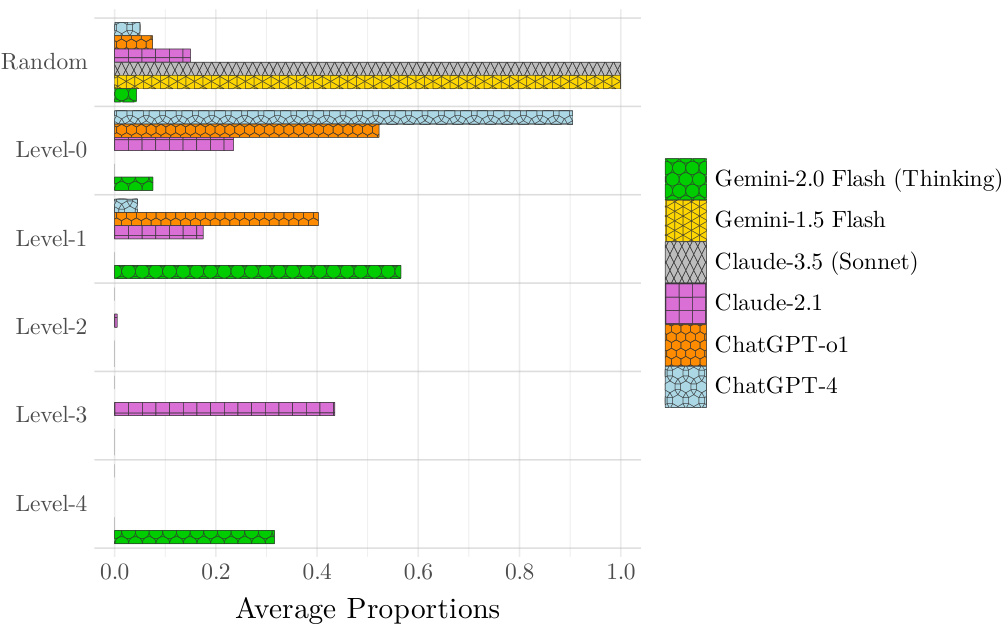
• 内容说明：直观比较不同LLM的MRG中各level-k类型比例。

- 解读：
- 标准LLMs（如GPT-4）随机与L0层响应比例偏高。
- Cl-2表现异常突出，甚至优于部分推理型LLMs。
- GPT-o1和Ge-2T推理步数较多，但整体仍低于人类基线。

3.6 附录B中的图B1 — MRG（游戏3）level-k分析

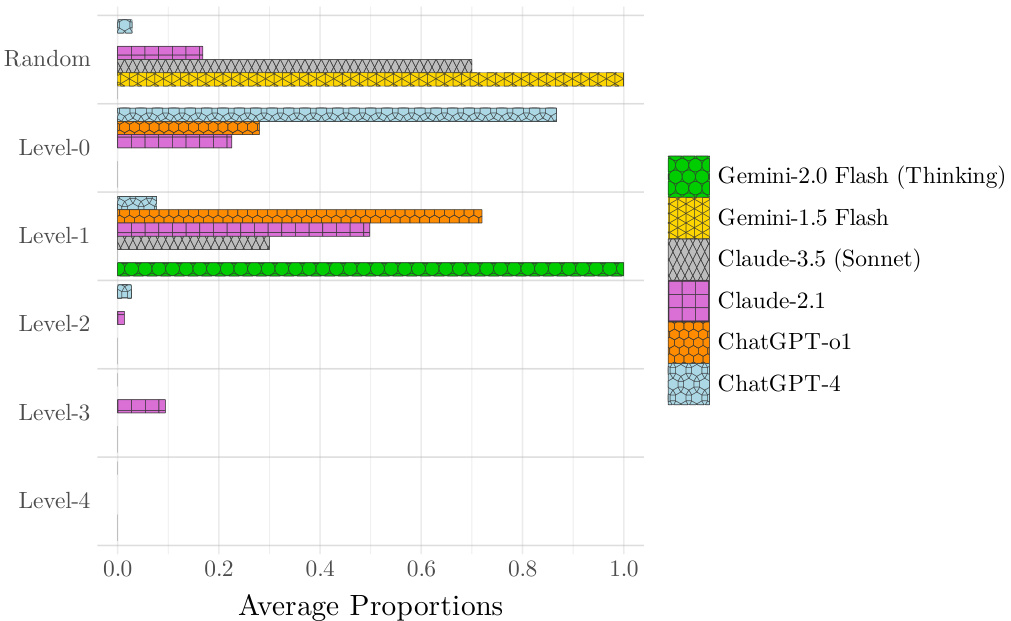
• 指出在较简单的MRG版本中，某些推理LLMs（GPT-o1）战略推理小幅提高。

- 人类实验水平依然明显优于LLMs。

3.7 其他温度敏感性测试图示（图B2、B3、B4、B5、B6、B7）

• 通过调节随机生成温度，LLMs的战略推理表现保持稳定。

- 高温增加回答多样性与偶发不连贯答案，低温减少多样性，结果整体模型结构推理深度结果无显著变化，表明战略推理鲁棒。

---

4. 估值分析与方法细节

• 使用最大似然估计（MLE）对Layer-k模型中各层级响应概率分布进行参数拟合。

- Level-k模型假设LLM响应为其层级对应理论行动附近的加噪声行为。噪声用离散对称分布模拟（近似二项分布）。

• CH模型通过Poisson分布参数τ统一拟合不同低层级混合权重。

- GG数据采用16轮连续响应，基于每轮对应特定参数集进行个别层级噪声最大似然估计。

• MRG模型无纯纳什均衡，因此level-∞层用L4层代表最高推理层，且明确区分随机型与非战略型行为。

- 整套估计方法确保合理覆盖真实策略分布及响应噪声，可解读推理深度与群体复杂性差异。

---

5. 风险因素评估

报告并未专门罗列风险，但可推断如下隐含风险点：

• 训练数据与环境设定偏好（如pBCG中$p<1$偏多）导致模型对部分条件泛化与适应受限。

- 部分推理LLMs具体增强技术未公开透明，难以完全复现与验证。

• 层级理性模型假设人类与LLMs推理机制相似，但该理论模型本身有局限，可能低估或误判某些战略复杂性。

- 标准LLMs在无反馈的单次博弈环境表现弱，影响其多智能体环境实时交互可靠性。

---

6. 批判性视角与细微差别

• 尽管GPT-o1推理层次数显著领先，推理能力和适应能力优于其他模型，但其更优表现可能部分归功于大规模强化学习和链式推理训练，反映“训练方法”而非模型架构本质优越。

- 4/3的pBCG参数环境下普遍较差表现暴露出训练集数据局限带来的抗压迫泛化问题。

• 在MRG游戏中，表现最优者竟是部分标准LLMs（如Cl-2），说明推理增强不总是一致优势，可能对应特定博弈结构。

- 层级理性模型假设对手层级降低1步或满足Poisson分布，简化现实策略交互，可能导致现实中更复杂的战略互动被忽视。

• 不同游戏间策略推理表现存在差异，表明LLMs战略能力尚有变异性和边界，未表现出完整泛化的“通用战略推理”。

---

7. 结论性综合

本报告全面评测了六款大型语言模型在三类经典多智能体行为经济学游戏中的战略推理能力，使用科学的行为经济学层级理性模型及最大似然估计进行了深入的模型拟合与参数评估。核心结论包括：

• 战略推理能力的分水岭位于推理增强的训练手段：GPT-o1、Claude-3.5-Sonnet、Gemini 2.0 Flash Thinking等推理型LLMs因采用大规模强化学习和多步推理链条，在所有博弈中表现出远高于标准LLMs的战略深度和适应速度。

- GPT-o1表现尤为优异：其在pBCG和GG中展现的推理层级几乎达到，甚至超越人类实验数据的上限，且在重复游戏中收敛最快，反映最强的策略适应性。

• 标准LLMs多表现于低层级推理：尽管在单回合博弈中表现薄弱，但多回合反馈训练提升有限，说明其战略推理机制不足以实现高阶递归预期。

- 各游戏环境对LLMs的考察维度互补且全面：pBCG主要测试均值基准下的集体思考，GG涉及异质目标区间的二人博弈，MRG测试了无纯纳什均衡的策略复杂性，三类游戏共同证实规律。

• 温度调整验证推理能力鲁棒性：在规划随机程度的温度参数调整后，LLMs的战略推理层次表现基本稳定，强化了结果的可重复性和普适性。

报告通过结合实验经济学严谨理论与前沿LLM评估，深入揭示战略推理的自然涌现与制约因素，强调专门推理训练对AI多智能体交互能力的决定性作用。对于未来Agentic AI与AGI系统的战略推理模块设计，具有极高的参考价值和指导意义。[page::0~53]

---

总结

此报告以科学而系统的行为经济学框架，结合最大似然估计严密统计方法，全面剖析了大型语言模型战略推理能力的层级与质量差异。其核心成果是，战略推理不仅是LLM能力的自然拓展，更关键依赖先进的推理增强训练机制，凸显未来AI智能体设计路径。图表数据佐证了这一观点，显示推理模型在战略游戏内拥有显著更高水平的认知层级，且能快速适应多轮反馈环境，而标准LLMs表现落后，人类被作为有力参考基准。此研究填补了对LLM战略思维能力实证评估的空白，为AI多智能体互动理论研究提供了坚实基础。

---

该详尽解构力求涵盖报告的每一个论点、模型细节、数据含义、方法推导及实验设计，满足内容系统性、专业性和深度分析需求。希望助力理解报告对未来AI战略推理领域的深远影响。

报告