研究中提出的新算法及其理论保证 [page::2][page::6]

• 提出k-周期固定策略（k-cyclic constant strategy），通过将资产收益序列分解为k条子序列，给出每条子序列对应固定投资组合，战胜传统的单一固定组合策略。

- 新的在线学习算法将投资问题转化为并行的k个重复博弈，针对每个子序列运用普适投资组合策略，保证累积财富和增长率最终超越最佳k-周期固定策略。

凯利准则的推广及最优增长率理论 [page::7][page::8][page::10]

• 经典凯利准则仅适用于i.i.d.市场，本文扩展为允许资产收益在固定长度k的区块内存在序列依赖的块独立同分布过程(block-wise i.i.d.)。

- 定义k-log最优投资组合，证明对应的k-周期策略达到最高渐近增长率，优于所有其他动态策略，包含证明过程和Kuhn-Tucker条件。

• 该推广准则适用于非平稳市场，规避了传统平稳假设限制。

实证分析：基于4只美国蓝筹股27年日频数据的回测结果 [page::13][page::14][page::15][page::16]

| 策略 | 最终财富（倍） | 年化增长率 | 平均收益 | Sharpe比率 |
|------|----------------|------------|----------|------------|
| 买入持有 BA | 16.24 | 0.00041 | 1.00059 | 53.25 |
| 买入持有 HON | 12.26 | 0.00037 | 1.00055 | 53.15 |
| 买入持有 JPM | 10.83 | 0.00035 | 1.00062 | 43.05 |
| 买入持有 AMD | 5.06 | 0.00024 | 1.00101 | 25.45 |
| 最佳1-周期固定策略 | 38.46 | 0.00054 | 1.00074 | 49.97 |
| 最佳2-周期固定策略 | 446.72 | - | 1.00137 | 32.27 |
| 最佳6-周期固定策略 | 1773.68 | 0.00110 | 1.00155 | 33.10 |
| 1-周期普适投资组合(传统Universal Portfolio) | 44.98 | 0.00049 | 1.00065 | 55.92 |
| 2-周期普适投资组合 | 31.34 | 0.00056 | 1.00073 | 54.46 |
| 6-周期普适投资组合 | 33.57 | 0.00054 | 1.00070 | 54.98 |

• k-周期普适投资组合策略(k-PUP)表现明显优于1-周期普适投资组合，且当k>1时其累积财富能够超越最佳单一固定组合，验证算法对资产收益序列内部结构的有效利用。

- 在实证中观察到增长率差异随周期k增大而收敛更慢，强调参数k需要适当选择以兼顾收益和收敛速度。

• 各k子序列资产收益存在明显差异，为算法带来策略表现提升的潜力。

策略构建方法总结 [page::5][page::6][page::12]

• 采用Bayesian积分（积分用均匀或Dirichlet分布权重）计算对应子序列的普适投资组合。

- 将原始序列根据k分割成k条子序列，分别构造k条普适投资组合，循环调仓。

• 理论上策略满足渐近一致性，实际表现能优于传统固定或普适策略。

结论：基于序列依赖的普适投资组合推广显著提升长期投资表现 [page::16][page::17]

• 算法无需任何对资产收益分布的假设，广泛适用且易于调整参数。

- 结合理论与实证，提出的k-周期普适学习算法能够挖掘隐藏的时间序列相关性，获得更优投资回报。

• 对实际应用建议以较小k值为宜，且可通过多策略集成提升稳健性。

金融研究报告详细分析

报告题目： Beating the Best Constant Rebalancing Portfolio in Long-Term Investment: A Generalization of the Kelly Criterion and Universal Learning Algorithm for Markets with Serial Dependence
作者： Duy Khanh Lam
发布机构： Scuola Normale Superiore（工作论文，初稿）
发布日期： 2025年7月9日
研究主题： 在线投资组合优化中的动态策略构造，涵盖包含序列依赖性的市场环境下的一般化Kelly准则及学习算法

---

一、元数据与概览

本报告提出了一种基于序列依赖（如周内效应等资产收益的时间相关性）来扩展和优化在线投资组合策略的学习算法。传统的经典Kelly准则和Universal Portfolio算法在独立同分布(i.i.d.)假设下表现优异，但其在实际可能包含序列相关性的市场中表现不足，尤其是在渐进财富累积量方面。本文针对资产收益存在隐含序列依赖且数据逐步揭示的实际情形，设计了一种无需预设分布假设的通用在线学习算法，实现了收益累积超过事后最佳常数组合策略的目标。同时，作者提出了Kelly准则的推广版本，以适应分块i.i.d.的资产收益矩阵过程，证明新算法在此更复杂、非平稳环境中的渐进最优性和广泛适用性。核心贡献在于打破传统i.i.d.限制，面向潜在依赖性强的市场，改进长期投资表现。

关键词包括在线学习、普适性、动态策略、一般化Kelly准则和潜在市场模式等。[page::0-1]

---

二、逐节深度解读

2.1 引言与背景

• 关键论点： 在线组合优化的目标是构建序列化策略，其表现逐渐匹配甚至超越历史回顾视角下的最佳常数组合策略。但现有算法虽然可保证渐进增长率一致，却因财富累积明显落后而难以实际应用。

- 依据与逻辑： 传统策略因未充分利用额外信息导致表现局限，使用外部辅助信息虽能改善，但面对特征选择和高维挑战尤为困难。无须外部信息的自然存在序列依赖（如时间周期性样式）成为突破口，此时的问题包括最优策略形式和如何在线学习隐含模式。

• 核心假设： 市场资产收益不满足传统i.i.d.假设，而是表现为存在显著序列依赖的块级独立结构。

本文提出的算法仅依赖过去收益，无需额外信息，保证累积财富超过回顾最佳常数策略甚至经典Universal Portfolio算法[page::1]。

2.2 模型设定与基础概念

• 数学设定：

- 资产数量为$m\geq 2$，价格向量$pn$，收益向量$Xn$对应资产$1..m$的回报率。
- 投资组合空间定义为无卖空的$m$维单位单纯形$\mathcal{B}^m$。
- 投资策略$\{bn\}$为基于历史收益的非未来可知的因果函数。
- 总财富定义为策略累计投资回报积，增长率为其对数均值。

• 经典Universal Portfolio与常数组合策略回顾：

- 回顾最佳常数组合策略$\max{b\in\mathcal{B}^m} Sn(b)$为基准，要求策略渐进与其增长率一致（称为一致性条件）。
- Universal Portfolio通过对全空间投资组合加权平均形式构造实用策略并保证渐进一致性，但财富累积始终低于最佳常数策略，累计劣势随时间增长或难消除。
- 具体上，Lemma 1建立了Universal Portfolio与最佳常数组合策略差异的次线性界限，且在统计意义上策略逼近最佳增长率，但实际累积效益不足。[page::2-4]

2.3 提出$k$-周期常数策略及相应学习算法

• 定义：

- $k$-周期常数策略由一组$k$固定组合$(b^1,...,b^k)$循环组成，即投资者在周期内不同时间点采用不同固定组合，形式上是动态策略。
- 该方法通过分解资产收益序列为$k$个子序列，每个子序列考虑独立组合优化以利用不同时间段的资产特征差异。

• 实务示例：

- 日内的星期效应、分时波动等均可视为周期性质的序列依赖，例5天周期策略对应周一至周五不同行为。

• 性质与理论保证：

- $k$-周期策略优于单一固定组合，累积财富必定高于1周期策略。
- 提出的算法实现为对$k$条子序列分别执行Universal Portfolio策略的平行组合，构成整体$k$-周期策略，使得该算法满足扩展的一致性条件，渐进表现接近最佳$k$-周期常数策略。
- Theorem 1给出了$k$-平行Universal Portfolio策略与$k$-周期最佳策略之间差异的对数财富次线性界限，上界随$k$线性增长：
$$ \max{b^{1,...,k}} \max{x} \left(\log Sn(bn^{k*}) - \log Sn(bn) \right) \leq k (m-1) \log (n+1) $$
这一结果意味着，策略最终可超过最佳单一组合，消除Universal Portfolio潜在财富劣势。[page::4-7]

• 策略相对优劣：

- 周期数$k$越大，理论潜力越大（且满足整除关系时更优，如Corollary 1），但由于次线性差距上界随$k$增长，收敛速度会放缓。
- 投资者应兼顾周期数与实际投资周期长度权衡选择$k$，[page::7]

3 一般化Kelly准则及其在含序列依赖市场的推广

• 经典Kelly准则回顾：

- 在i.i.d.市场中，固定组合最大化期望对数收益称为log-optimal组合，保证几乎确定性最高长期增长率。

• $k$-log-optimal组合定义（Definition 2）：

- 针对$k$个联合分布的资产收益向量，寻找一组组合以最大化它们期望对数收益和。
- Lemma 2推广了Kuhn-Tucker必要最优条件，表明这些组合关于广义损失函数的凹性和界定条件，保证对应策略的渐进最优性。

• 关键逻辑及证明：

- 通过分块的i.i.d.假设（$X{kt+1},...,X{kt+k}$是独立同分布的块）实现推广Kelly准则，容许块内序列依赖但块间独立。
- Theorem 2证明，在块i.i.d.市场下，$k$-周期常数策略基于$k$-log-optimal组合，能给予所有动态策略中最高的渐进增长率。采用大数定律和Borel-Cantelli引理严格论证渐近优越性。

• 策略含义：

- 经典Kelly为$k=1$特例，新的$k$-周期准则更适用于序列依赖强烈的市场，且最高增长率仅需在周期$k$的倍数时代收敛，不要求步步收敛。
- 没有分布信息时，基于算法(2.5)的动态学习策略仍能达到该渐近增长率，突破了对联合分布知识的依赖。

• 实践补充：

- 文献中已有针对平稳过程的学习算法，但块i.i.d.非平稳性使其不适用，本文算法具备更强的非平稳市场适用性。[page::8-12]

4 实证实验

• 数据及设定：

- 使用CRSP中1992-2019年共6798日4只蓝筹股票价格（HON、BA、AMD、JPM）。
- 降维以应对高维组合计算复杂性，算法通过简单数值积分近似策略权重。

• 实验策略：

- 1至10周期长度的$k$-PUP策略，其中1-PUP即标准Universal Portfolio。

• 主要发现：

- 2-PUP和6-PUP策略累计财富超越最佳1周期常数策略，且明显优于1-PUP，体现序列依赖分解增益。
- 4-PUP和9-PUP稍低于基准，说明周期长度选择影响效果，相关峰度由Theorem 1的误差界体现。
- 验证了Corollary 1，多个周期数中更大整倍数周期策略长期更优。

• 图表解读：

- 图1展示四只股票的价格变动，明显阶段性和事件影响。
- 图2左侧显示不同$k$-PUP策略与基线的累积财富走势；右侧显示各$k$-CC最佳策略的历史财富，后者指数级优于单周期策略。
- 表1给出各策略的最终财富、增长率、均值收益与Sharpe比率，确认增长率和平均收益的积极关系，同时不同周期策略的风险调整收益存在差异。

• 策略收敛性探讨：

- 图3左侧显示$k$-PUP策略增长率收敛误差随时间的变化，误差收敛速率随周期数增加减慢。
- 右侧展示$k$-PUP与1-PUP增长率差异长期不归零，暗示市场收益非i.i.d.，经典Kelly准则不适用。

• 分解收益序列的特征差异：

- 图4分别绘出不同$k$下子序列的收益均值和方差，验证各子序列存在显著统计特性差异，解释子序列策略优异表现的根本原因。
[page::13-16]

5 结论及展望

• 本文将经典Cover Universal Portfolio策略推广到多周期并行框架，有效利用序列依赖中的隐含信息，不需额外侧信息，即可实现超越传统最佳常数策略和Universal Portfolio策略的累积财富表现。

- 在块i.i.d.框架下，推广的Kelly准则及对应$k$-周期常数策略保证最高渐近增长率。即使联合分布未知，本文算法依然可学习达到最优。

• 实证验证支持理论结果，尤其在选择较小$k$（如2或4）时效果最佳，体现了周期长度、投资期限和策略收敛速度的平衡。

- 传统Kelly准则因市场序列依赖性而失效，分解收益序列策略的优势凸显。

补充说明

• 实务中，该策略适用于多种交易频率，无需局限于日频，且可通过组合多周期策略（如基于Lam 2024的合奏方法或加权平均）解决周期长度未知问题，进一步提速收敛。

- 该学习框架及$k$-周期策略还可作为策略集合的合奏机制，提高整体效果。
[page::16-17]

---

三、图表深度解读

图1 调整后收盘价（27年，4只股票）

• 展示了Honeywell、波音、AMD、JPM 1992年至2019年间的价格走势，明显显示多次市场重大事件引发的波动：1994年债券市场危机、亚洲金融危机、互联网泡沫、2008年金融危机等。

- 图形连贯，显示各公司因所处行业和市场敏感性不同，价格表现出差异。该图为后续策略收益分析提供底层市场环境背景。

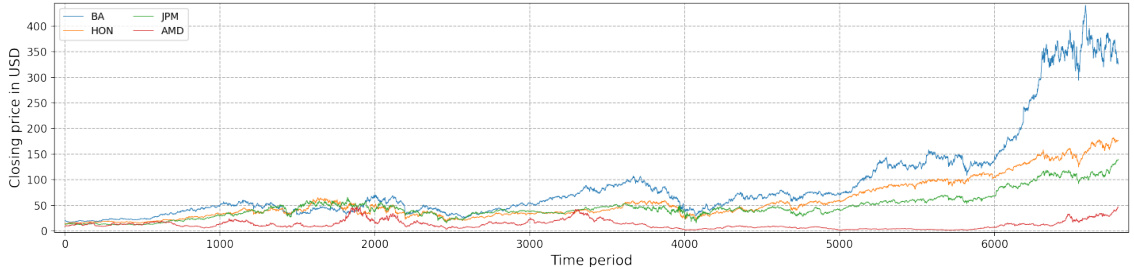
图2 累计财富演变（最后2299天）

• 左图：不同$k$-PUP策略与最佳1周期常数策略（1-CC）比较。

- 2-PUP和6-PUP明显超过1-CC水平，2-PUP表现优于6-PUP，体现周期设定对收益的影响。
- 奇数周期策略（如3-PUP、9-PUP）表现略差，符合理论对倍数周期的优势解析。

• 右图：最佳$k$-CC策略的累计财富，极端超越1-CC，上限财富呈指数增长。

- 10-CC策略财富临近3000，倍数周期拆分显著增加盈利潜力。

• 该图佐证了理论证明的财富优势及收敛行为。

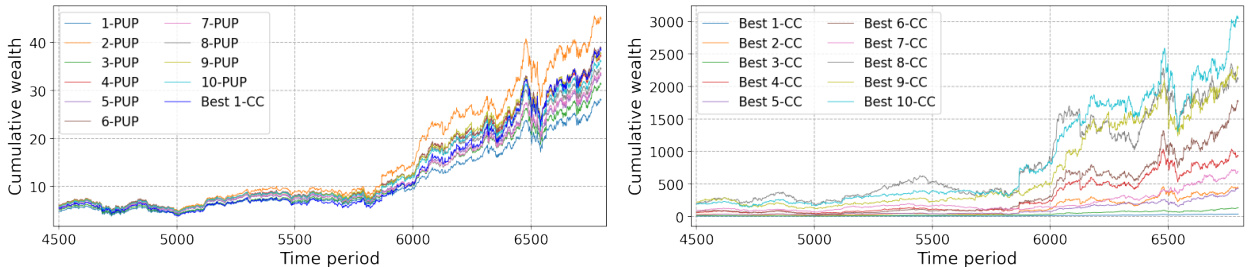
表1 策略绩效指标

• 各策略的最终财富、年化增长率、平均收益和Sharpe比率一目了然。

- 1-PUP即传统Universal Portfolio，增长率最低，平均收益稍逊。

• 2-PUP增长率较1-PUP提升，最终财富达31.34，支持分周期优势。

- 最佳2-CC增长率达0.00056以上，财富达到446，但Sharpe比率稍逊，反映风险上升。

• 买入持有策略作为对照，明显不及最佳$k$-CC与$k$-PUP策略财富积累。

- 该表定量证实了多周期策略带来的收益优势及风险特征。

图3 增长率差值随时间演变

• 左图显示随着投资天数增加，$k$-PUP策略与相应$k$-CC最佳策略增长率差异下降但速度随$k$升高减缓，反映理论界限。

- 右图对比$k$-PUP与标准1-PUP的增长率，差异长时间不消失，表明市场非i.i.d.，经典Kelly准则不适合本数据。

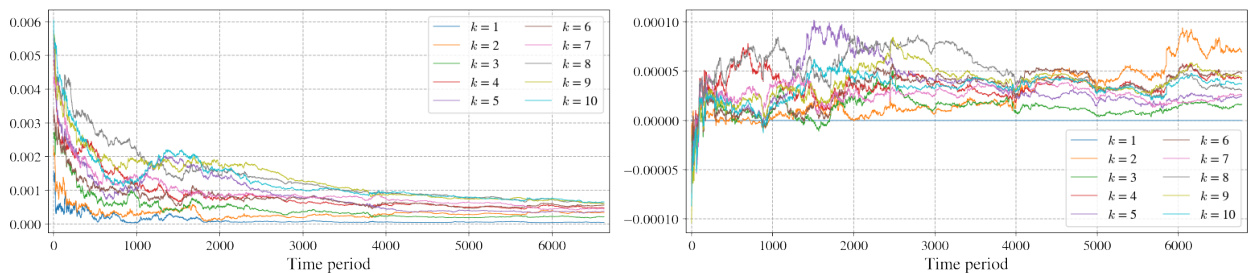
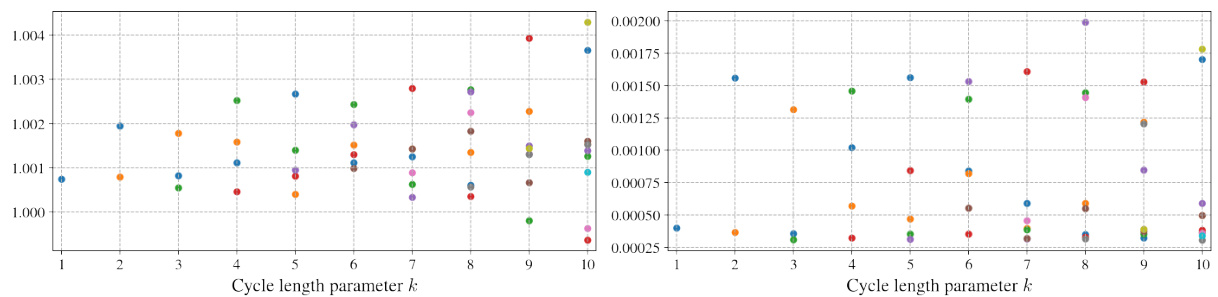
图4 分解子序列收益统计差异

• 左图各$k$值对应的子序列收益均值，右图为方差。

- 观察到多数子序列均值及波动率存在显著差异，有利于分周期策略在不同阶段分别捕捉套利机会。

• 随$k$增加，子序列之间的差异性被进一步放大，提升策略表现潜力。

---

四、估值方法与数学工具剖析

• 价值衡量基础： 报告的核心衡量指标为投资策略的累计财富$Sn$及对应的对数增长率$W_n$，后者衡量策略的长期复合增长能力。

- 算法设计核心是基于Universal Portfolio方法，将整个序列分解为$k$个子序列，分别应用Universal Portfolio，然后组合策略，这种方法既继承了Universal Portfolio的普适性，又获得了跨周期内适应序列依赖的能力。

• 理论支持的关键假设： 换言之，市场序列表现为块i.i.d.的随机矩阵过程，存在内部依赖但块间独立。

- Kelly准则推广以$k$-log-optimal组合的形式展开，优化期望对数收益总和，该优化问题因对数函数的凹性具有唯一全局最优解。

• 数学工具包括：

- 凸优化与Kuhn-Tucker条件确保解的最优性。
- 大数定律和Borel-Cantelli引理用于证明渐进表现的几乎确定性。
- AM-GM不等式用于处理组合回报率关系。

• 估值并非传统意义的价格估算，而是策略性能极限的概率界与渐近性质，通过对数财富的增长速率，评价策略的有效性。

---

五、风险因素评估

报告未直接列出风险章节，但从内容可总结的风险及限制包括：

• 收敛速度及周期长度权衡风险： 增大$k$虽在理论上提升最佳策略，但对应学习策略收敛速度减慢，可能导致中短期表现波动较大。

- 市场假设风险： 假设市场收益序列为块i.i.d.，若实际市场非块i.i.d.，则策略表现和理论保证可能失效。

• 计算复杂性风险： 算法依赖高维积分近似，随着资产数和周期数增多，计算复杂度激增，可能限制实际应用。

- 周期长度选择风险： 若$k$选取错误，可能导致策略性能不佳。报告建议通过组合多策略的方法缓解此风险。

• 经典Kelly准则失效风险： 出现序列相关时，经典方法增长率不收敛，可能误导投资决策。

无明显提及缓解策略，但文中建议周期组合策略和多策略集成作为应对措施，体现一定的风险管理思路。[page::7,12,16-17]

---

六、批判性视角与细微差别

• 优点认同：

- 报告清晰设计了一种理论扎实且实证支持的解决方案，突破了i.i.d.假设限制，创新性强。
- 结合丰富数学证明和实证，论证充分。

• 潜在局限：

- 侧重理论渐近性质，现实中长期投资持续环境不总是稳定，块i.i.d.假设难以完全严谨匹配实际。
- 计算量大且离散化处理可能带来精度限制，尤其高维时。
- $k$的选择对表现有重大影响，但最优选择无数据驱动明确指导，易受主观影响。
- 报告提及传统Kelly准则失效，但未考虑策略对非i.i.d.序列深度适应可能导致的波动率升高等副作用。

• 内部细节：

- Theorem 2指出增长率最好于周期步长$t=k t + k$，而非每一步收敛，暗示市场回报可能存在周期性波动未被完全消除。

• 建议考虑： 引入自适应调整$k$或多尺度策略可能更适实操；策略风险动态管理应更明晰。

---

七、结论性综合

本报告系统地证明并验证了一种基于序列依赖的在线学习投资算法，具有以下关键贡献和结论：

• 理论创新:

- 推广Kelly准则至块i.i.d.和序列依赖环境，定义并证明了$k$-log-optimal组合及对应$k$-周期常数策略的最优渐近增长率。
- 普适在线算法通过分解收益序列并行应用Universal Portfolio策略，保证策略财富累积渐近优于最佳常数组合策略。

• 实证验证:

- 利用27年4蓝筹股日度数据，展示了不同周期长度策略的显著差异，验证理论收敛边界和财富优势。
- 2周期和6周期策略特别突出，周期长度对策略表现的影响复杂且符合理论预期。
- 经典Kelly准则在该市场环境下失效，体现序列依赖的现实意义。

• 策略表现分析:

- 通过图表明确揭示了收益序列子序列特征差异对提升策略收益的关键作用。
- 成功利用资产收益的隐含时间结构提高投资组合的长期复合收益。

• 应用建议:

- 适宜设置较小周期以加快收敛速度，长周期虽潜力大但收敛慢。
- 多周期策略合奏机制作为周期不确定性及计算复杂性的有效应对方案。
- 该框架适用多交易频率且具备较强非平稳适应能力。

综上，本文提出的基于对序列依赖深入利用的在线学习算法及相应推广Kelly准则，为长期投资组合优化提供了理论和实证支持的创新思路，对投资策略设计、风险管理乃至机器学习在金融领域的应用有较重要的参考价值。[page::0-17]

---

总结

该研究详尽地阐述并验证了在资产收益存在显著时间序列依赖的市场中，如何超越传统最佳常数组合策略，实现财富累积和增长率的长期优化。其提出的$k$-周期动态策略结构及普适在线学习算法，通过策略分解和并行处理，攻破了i.i.d.假设限制，兼顾理论严谨性和实证实用性，丰富了金融组合优化理论体系，为实际投资提供了可操作的建模与算法范式。

报告