对冲市场因子风险的谱残差定义与性质 [page::6][page::7]

• 谱残差通过PCA分解收益协方差矩阵，舍弃特征值最大的几个主成分，保留小特征值对应部分以剔除市场风险敞口。

- 理论证明谱残差与共同因子不相关，协方差矩阵近似对角，有利于残差信息的独立性体现。

• 谱残差的计算速度远快于因子分析（FA），PCA提取耗时约10分钟，FA约13小时。

基于分布预测的投资组合构建 [page::8][page::9]

• 利用分位数回归方法对谱残差未来收益分布进行条件分布预测，获得多个等距分位数估计。

- 通过分位数计算均值与方差估计，用于现代投资组合理论的最优权重求解，重点构建零投资组合。

• 提出两种神经网络架构设计：波动率（振幅）不变性利用正齐次函数框架；时间尺度不变性通过分形网络结合不同采样率序列的特征提取。

残差因子反转策略的实证对比 [page::11]

• 利用日本市场数据对比基于原始收益、FA残差和谱残差的简单反转策略。

- 谱残差和FA残差均表现出更强的稳健性，能有效对冲市场重大危机风险，夏普比率谱残差为2.86优于FA为2.64。

美国市场的策略性能评估 [page::12]

| 策略 | ASR↑ | AR↑ | AVOL↓ | DDR↑ | CR↑ | MDD↓ |
|------------|--------|---------|--------|--------|--------|--------|
| Market | 0.607 | 0.130 | 0.215 | 0.939 | 0.263 | 0.496 |
| AR(1) | 0.858 | 0.021 | 0.025 | 1.470 | 0.295 | 0.072 |
| Linear | 0.724 | 0.017 | 0.024 | 1.262 | 0.298 | 0.059 |
| MLP | 0.728 | 0.022 | 0.030 | 1.280 | 0.283 | 0.077 |
| SFM | 0.709 | 0.019 | 0.026 | 1.211 | 0.323 | 0.058 |
| DPO-NQ | 1.237 | 0.032 | 0.026 | 2.169 | 0.499 | 0.063 |
| DPO-NF | 1.284 | 0.027 | 0.021 | 2.347 | 0.627 | 0.042 |
| DPO-NV | 1.154 | 0.030 | 0.026 | 2.105 | 0.562 | 0.053 |
| DPO(提出) | 1.393 | 0.030 | 0.021 | 2.561 | 0.656 | 0.045 |

• 所提DPO模型综合测试区间收益、风险指标表现最佳；分布预测和分形网络结构显著提升了夏普比率。

- 归一化归因于降低模型自由度，提高样本效率与风险调整表现。

谱残差对策略性能提升的作用 [page::13]

• 移除谱残差后所有方法性能下降明显，弱化了反转现象的表现及夏普比率。

- 改进说明谱残差能有效抑制共同市场因子风险敞口，有效提升模型的稳健性和收益风险权衡。

基于残差因子分布预测的投资组合优化报告详尽解读

---

一、元数据与概览

• 报告标题： 基于残差因子分布预测的投资组合优化——“学海拾珠”系列之一百七十五

- 报告作者与机构： 杉（执业证书号：S0010522110001，邮箱：luoyushan@hazq.com）和严佳炜（执业证书号：S0010520070001，邮箱：yanjw@hazq.com），华安证券研究所发布

• 发布日期： 2024年

- 研究主体： 投资组合优化方法及其在股票市场（尤其美国和日本市场）上的应用验证

• 核心论点： 本文提出一种基于谱分解的“谱残差”因子，结合基于深度神经网络的分布预测方法，通过神经网络架构融入金融归纳偏差，实现更高效且稳健的投资组合优化。该策略不仅具有较快计算速度，还能更好对冲市场因子风险。

- 主要结论： 谱残差能有效解耦市场共同因子风险，分布预测结合特定网络架构提升投资组合的夏普比率等多项关键指标。实证测试表明新方法在美国和日本市场均取得显著优于传统方法的表现。

• 评级与建议： 报告以学术前沿研究为核心，未直接提供投资评级，仅提出风险提示，强调内容为方法论总结，不构成投资建议。[page::0]

---

二、逐节深度解读

1. 简介与背景 （第3-6页）

• 关键论点：

- 金融时间序列因其非静态、高波动和快速变化的特性，不适合直接应用传统机器学习的静态假设。
- 需引入具备“归纳偏差”的神经网络架构以加快适应市场环境变化。
- 股票市场表现出三大特点：残差因子可对冲时变风险敞口、存在振幅与时间尺度上的不变性、分布预测可用于理性投资组合构建。

• 推理依据：

- 市场因子通过历史文献支持（如Fama-French三因子模型）存在；残差因子被认为载有公司特定、非市场风险信息。
- 机器学习领域CNN和LSTM对静态环境的归纳验证以及金融序列波动聚集和分形结构的实证结果。
- 现代投资组合理论提供了均值-方差框架，分布预测能更细粒度地捕捉未来收益波动和不确定性，有助精细调优投资组合权重。

• 数据及概念：

- 股票收益 $r{i,t}=\sumk \betai^{(k)} ft^{(k)} + \varepsilon{i,t}$ 线性分解，其中 $\varepsilon{i,t}$ 为残差因子，表达非共同因子部分。
- 零投资组合被定义为多空头仓位净和为零，确保买卖平衡；报告重点构建此类组合，便于策略间的公平比较。

• 细节与概念阐释：

- 归纳偏差指神经网络设计时融入的数据不变量属性，帮助模型捕捉序列中固有特征，例：振幅不变性、时间尺度不变性。
- 动量与均值回归策略间的逻辑对立，现代组合理论提供统一框架将预测的收益与风险映射至投资权重。

2. 预备知识 — 投资组合形式化（第5-6页）

• 数学形式与符号定义：

- 股票价格序列 $\mathbf{p}^{(i)}$ 与根据价格计算的收益率 $rt^{(i)} = p{t+1}^{(i)}/pt^{(i)} - 1$。
- 投资组合权重向量 $\mathbf{b}t$ 满足总绝对权重和为1，且关注零投资组合（即净权重和为0）。
- 延迟参数$d$考虑了交易执行与收益观测间的时延，即使用 $r{t+d}^{(i)}$ 来计算$t$时刻组合收益。

• 投资优化的目标函数和指标（夏普比率）：

- 最大化风险调整收益被形式化为夏普比率公式，风险通过收益波动（标准差）度量，反映资金的收益效率。
- 经典马科维茨优化解 $\mathbf{b}^* = \lambda^{-1} \Sigma^{-1} \mu$，其中 $\Sigma$ 是协方差矩阵，$\mu$ 是收益均值向量，$\lambda$ 为风险厌恶参数。

3. 系统架构（第6-10页）

• 系统模块划分：

(i) 提取残差因子（谱残差）以对冲共同市场因子风险。
(ii) 使用神经网络预测残差因子的未来条件分布。
(iii) 基于分布预测结合现代组合理论构建最优投资组合。

• 3.1 谱残差定义与理论基础（页6-7）：

- 通过协方差矩阵的特征分解和主成分分析，选择舍弃特征值较大的主成分对应的主要投资组合，保留低特征值主要成分的收益组成谱残差。
- 投影矩阵 $At = Vt \text{diag}(0,...,0,1,...,1)Vt^\top$实现上述筛选。
- 理论证明谱残差与共同因子无相关性，协方差矩阵近似对角化，即残差因子相互独立。
- 相比传统因子分析法（FA），谱残差的计算速度极快（大规模市场数据计算时间从13小时缩减到10分钟），且表现出良好对冲能力。

• 3.2 分布预测与投资组合构建（页8-9）：

- 通过分位数回归方法，预测未来剩余收益的多个等距条件分位数 ($\alphaj = j/Q$)，实现对残差因子未来分布的非参数估计。
- 利用得到的分位数序列估算未来均值和方差，结合现代投资组合理论导出资产权重表达式。
- 预测和权重计算体系内嵌梯度计算，可支持端到端训练。

• 3.3 网络架构设计（页9-10）：

- 两大核心金融归纳偏差嵌入网络设计：
- 波动率不变性：采用正齐次函数模型确保模型输出对振幅缩放保持正比响应，即输入信号乘以正数不改变结构，提升对波动聚集效应的稳健性。
- 时间尺度不变性（分形结构）：采用“分形网络”，通过不同采样率的子序列得到多尺度信息，融合处理以利用时间序列的自相似性，从而提高采样效率和网络泛化能力。
- 具体实现为先通过重采样模块产生多尺度序列，再由两个深度网络$\psi1$和$\psi_2$分别提取与整合信息。

4. 实验与效果验证（第11-13页）

• 4.1 数据描述与通用设置：

- 使用S&P 500成分股2000至2020年4月的每日开盘价，2008年前数据训练验证，2008年后测试。数据由Alpha Vantage提供。
- 采用延迟$d=1$，回溯窗口长度$H=256$交易日，确保模型利用近期长期信息。
- 关键评估指标包括累计财富（CW）、年化收益率（AR）、年化波动率（AVOL）、年化夏普比率（ASR）、最大回撤（MDD）等。

• 4.2 谱残差的有效性验证：

- 与基于原始收益及传统因子分析残差因子（FA residuals）策略对比，采用简单反转策略测试因子效用。
- 图表3显示，基于谱残差和FA的交易策略在经历三次重大金融危机（互联网泡沫、次贷危机、2020年股市崩盘）期间表现更稳健，累计收益更高。
- 夏普比率谱残差2.86优于FA残差2.64，且计算速度显著领先，验证谱残差的有效性与高效性。

• 4.3 综合系统性能评估与消融实验：

- 相较多基线方法（Market，AR(1)，线性回归，MLP，SFM），研究所提出的深度组合优化（DPO）系统表现最优。
- 分布预测（与均值回归对比）显著提升夏普比率，且兼顾收益和风险的平衡。
- 分形网络及振幅归一化进一步优化风险调整收益性能，降低波动。
- 谱残差的引入对所有模型均有效提升性能，特别是鼓励反转现象，抑制共同市场因子造成的相关风险敞口。

• 图表解读：

- 图3（第11页）展示三类因子对应策略累计收益，谱残差及FA残差波动时更加稳健且收益领先原始收益。
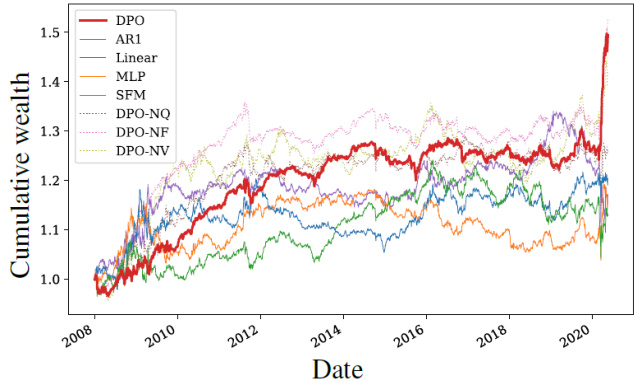
- 图4（第12页）为不同策略累计财富走势，DPO曲线显著高于其它方法。
- 图5提供量化比较指标，DPO夏普比率最高达1.393，且最大回撤较小，Calmar比率等指标均优于基线。
- 图6-7（第13页）为未提取谱残差修正版本，展示谱残差对性能带来的提升。

---

三、图表深度解读

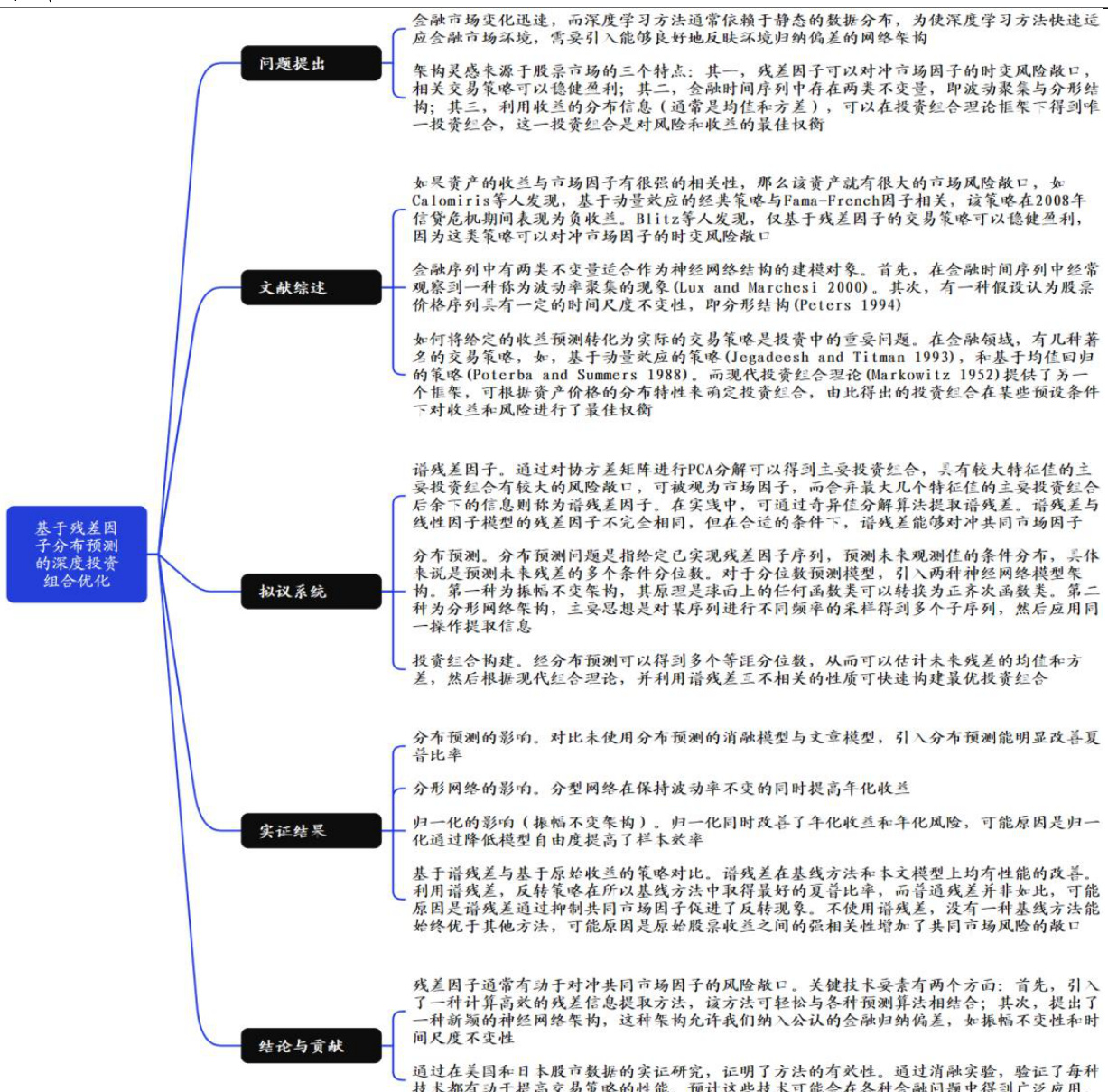
图表 1：文章框架（第3页）

• 系统性梳理了研究问题提出、文献回顾、残差因子构造、分布预测、实证结果与结论贡献五大环节，强调理论方法与实证验证相结合的整体逻辑。

- 图表框架清晰反映了如何通过残差对冲和网络预测相结合构建稳健投资策略的思路。

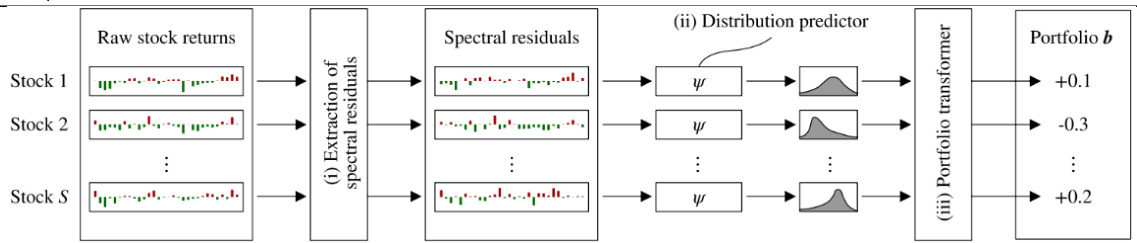
图表 2：系统概述图（第6页）

• 描绘了系统流程的三个核心步骤：

原始股票收益→残差因子提取（谱残差）→分布预测→投资组合权重输出

• 体现了流程中核心模块关联，并展示了预测输出到权重转化的闭环结构，方便读者理解模型架构与信息流。

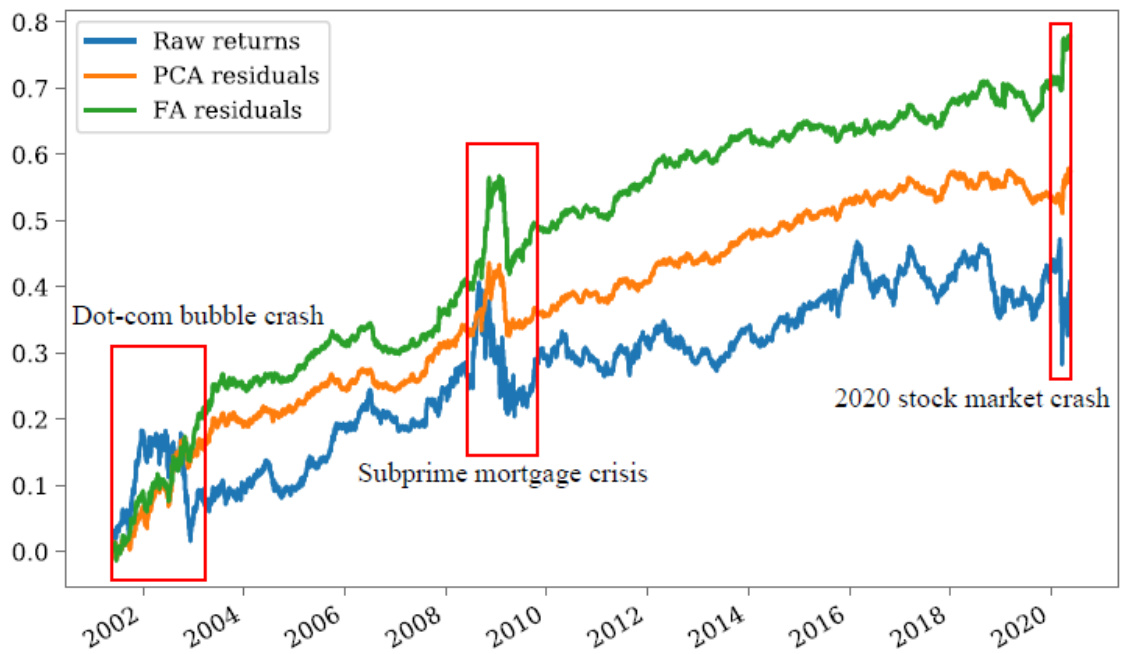
图表 3：反转策略的累积收益率（第11页）

• 显示基于原始收益、FA残差及谱残差三类因子的反转策略累计表现。

- 观察到原始收益受重大金融危机冲击显著，表现不稳；谱残差和FA残差策略波动小，收益连续性好。

• 特殊标注三个危机事件位置，强调残差策略对风险敞口的对冲能力。

- 该图形视觉支持删除极大特征与风险因子带来策略稳健性的最核心观点。

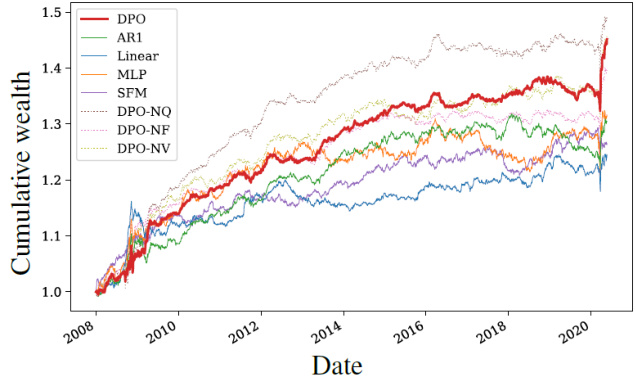
图表 4-5：美国市场策略表现（第12页）

• 图4曲线显示DPO策略累计财富最高，且其增加趋势稳健，区别于基线策略波动较大及收益较低。

- 图5详细指标表格，支持文本分析：DPO夏普比率1.393显著优于市场基线0.607，以及波动率、最大回撤等关键风险指标均优化。

• 消融实验清晰体现分布预测、分形网络和归一化对性能提升的贡献程度。

图表 6-7：未使用谱残差的策略表现（第13页）

• 对比使用谱残差后的图表4-5，整体表现显著弱化，突出谱残差对提升策略鲁棒性和收益风险平衡的重要作用。

---

四、估值分析

本报告主要聚焦于量化交易策略方法及其实证绩效，不涉及公司估值或股票定价模型。投资组合权重构造基于经典的马科维茨均值-方差最优化框架，辅以预测残差因子收益分布实现收益-风险平衡优化。故不涉及估值方法论。

---

五、风险因素评估

• 基于历史和海外文献： 报告风险提示明确说明所提方法依赖历史数据和国外实证研究，不能直接作为投资建议。

- 市场动态复杂性： 金融市场的非静态和复杂性可能影响模型泛化能力，且历史表现不代表未来收益。

• 模型参数及实施风险： 参数选择（如残差因子数量C，窗口长度H）对策略表现有较大影响，且执行延迟和交易成本未被充分讨论。

- 归纳偏差假设风险： 振幅与时间尺度不变性的假设，虽基于实证，但如果市场结构发生根本变化，模型性能可能下降。

• 神经网络模型风险： 深度学习模型可能出现过拟合，对数据依赖性强，且风险管理不足可能导致异常时点损失。

目前报告中对缓解策略未明示，仅以实验结果和理论证明作为支撑。

---

六、批判性视角与细微差别

• 深度模型的可解释性与稳健性问题： 虽然引入了归纳偏差建模，但神经网络模型的黑箱特性未在报告中有针对的剖析，对因果关系理解有限。

- 残差因子定义与计算简化： 虽然谱残差计算效率高，但是否完全捕捉所有有价值的残差信息仍有讨论余地，因PCA线性假设与金融时间序列非线性特性可能存在冲突。

• 数据集限制： 主要聚焦于美国和日本成熟市场，对于新兴市场和不同资产类别测试不足，结果的普适性和稳健性需谨慎看待。

- 投资实际执行延迟的影响： 报告考虑了延迟参数，但未深入探讨交易成本、流动性等现实因素对策略绩效的影响。

• 表述谨慎且未过度推销，风险提示明确，体现了客观实事求是的态度。

---

七、结论性综合

本文系统提出并验证了一种基于谱残差因子分布预测进行投资组合优化的新型量化策略体系，主要技术亮点包括：

• 利用主成分分析剔除大型共同市场因子，定义谱残差因子，有效降低市场风险敞口，且显著提升计算效率（从FA的13小时降至10分钟）。

- 借助分位数回归方法精准预测残差因子未来收益分布的多个条件分位数，非参数地反映收益的偏斜与多样性特征。

• 创新融合金融序列表现出的振幅不变性与时间尺度不变性，设计双网络分形架构，有效提升模型泛化能力与样本效率。

- 结合现代投资组合理论，利用预测分布的均值及方差估计构造风险最优投资组合，重点关注零投资组合以公平比较各策略。

• 实证分析显示，该方法在美国和日本股市实测中均超过多项基准与先进机器学习模型，表现为更高夏普比率、累计财富及更低回撤，尤其在重大金融危机中稳定性优异。

- 消融试验进一步证实分布预测、分形网络和振幅归一化均为提升绩效的关键因素。

• 报告严谨披露方法基于历史数据与国外文献，明确不构成绝对投资建议，提醒投资者审慎决策。

总体而言，本报告表现出作者对新兴深度组合优化技术的深入理解，详细解释了数学基础与架构设计，并通过丰富实证验证了该方法的前沿有效性，较好承接了理论与实践的桥梁作用。谱残差作为高效对冲市场风险的创新因子提取方式，结合针对金融市场特性的神经网络设计，为未来量化交易研究和实践提供了重要参考路径和技术手段。

---

附：关键图表的Markdown形式引用示例

• 图表1 文章框架

• 图表2 系统架构

• 图表3 反转策略累计收益率对比

• 图表4 策略累积财富（美国市场）

• 图表6 策略累积财富（未提取谱残差）

---

以上是对报告的详细分析及充分解读，涵盖结构、论点、数据、图表及风险等多维度，确保内容客观专业，全面深入。[page::0,3,4,5,6,7,8,9,10,11,12,13,14]

报告