Bermudan Swaption定价模型创新 [page::0][page::1]

• 引入无需产品特定校准的半解析定价方法，基于掉期利率及相关性而非均值回复参数。

- 以midcurve swaptions及相对行权价swaption为桥梁，构建模型框架。

• 模型支持利率相关产品纳入对冲组合以改进风险管理。

Midcurve Swaption与相对行权价Swaption定价机制 [page::1][page::2][page::4]

• Midcurve swaption视作长短期掉期利率相关加权组合的期权。

- 通过copula积分计算，权重由掉期年金比例决定，支持随机年金比率的线性化处理。

• 相对行权价swaption中行权价基于先行定价，实现了波动率替代和相关性分析。

Canary Swaption模型及Gaussian假设下解析解 [page::6][page::7][page::8]

• Canary swaption为仅含两个行权日的简化Bermudan swaption。

- 利用联合高斯分布及交换率相关性，推导出解析定价公式。

• 对假设完美相关性条件下的价格给出闭式表达。

- 通过双重积分与矩匹配方法，展示与市场报价的拟合效果。

Bermudan Swaption的递归定价及相关性矩阵构建 [page::9][page::10][page::11]

• 通过逐步倒推的方法将Bermudan swaption分解为多层Canary swaption组合。

- 计算联合分布和条件期望，构造行权日期间的相关性矩阵，便于高维积分。

• 在完美相关假设下，利用矩匹配技术有效计算最大值期权。

Hagan LGM格点模型扩展与随机年金比例调整 [page::11][page::13]

• 提供类LGM格点定价框架，结合条件期望函数回溯计算。

- 引入调整参数实现随机年金比例的凸性校正，提升模型灵活性及准确度。

• 市场验证表明新格点模型对市场数据的拟合优于经典Hagan LGM模型。

模型结论与应用前景 [page::14]

• 模型明确展示了Bermudan swaption定价对利率分布和相关性的依赖，避免了难以观测的模型参数校准。

- 提供多种实际可用的估值方法，适合快速风险管理。

• 建议保持市场中Bermudans、midcurves与相对行权价swaption间的动态调整以满足定价一致性需求。

财务报告深度分析报告：Berms without Calibration

---

1. 元数据与概览

• 标题：《Berms without Calibration》

- 作者：K. E. Feldman

• 发布机构：Scotiabank: Innovation Hub

- 时间：文中无具体发布日期，但引用文献中有2020-2021年，且图表为2025年市场环境，推测为近期研究。

• 研究主题：本报告针对金融衍生品利率期权中的Bermudan swaption（半年度或多期权行权利率互换期权）提出了一种无需产品特定校准的新定价模型。其核心关注点是基于各种期限结构swap rates分布和它们之间的相关性，不依赖传统难以观测的参数如均值回复率（mean reversion）进行定价。

报告核心论点与贡献：

• 传统Bermudan swaption定价模型中，需校准隐含波动率曲线和均值回复，并依赖特定期限结构模型如Hull-White或LGM (Linear Gaussian Model)。此过程复杂且难以估计关键参数。

- 本文构建的半解析模型通过变更计量资产（numeraire）至相关掉期期权的年金，从而将传统上难以观测的均值回复参数替换为可从历史或市场数据（midcurve swaptions 与 CMS spreads）估计的swap rates相关性，实现无产品校准的定价与风险管理。

• 阐述了midcurve swaption、具有相对行权价的swaption与Bermudan swaption的内在联系，尤其通过解析最简单的“Canary” swaption（二选一行权日期的Bermudan）为切入点，逐步推广到一般Bermudan定价。

- 最终报告提出的模型可实现在匹配市场实际条件下的快速且准确的定价和风险管理。

该报告在衍生品定价理论和实际风险管理中均具备突破意义，表明了一种更为简洁和稳健的定价体系。

---

2. 逐节深度解读

1. 引言（Introduction）

论点与信息：

• 介绍Bermudan swaption的产品定义和传统定价依赖（Hull-White过程，LGM模型，基于隐含波动率和均值回复参数）。

- 均值回复参数在理论中关联转期波动率（forward volatility），但该参数难以直接从市场流动产品中估计。

• 中间期限swaption（midcurve swaption）被视为理解forward volatility曲线的关键，但整合入传统期限结构模型较为复杂。

- 本文目的：直接连接Bermudan swaption和midcurve swaption，通过“带相对行权价的swaption”作为桥梁，构建无需特定产品校准的新模型。

• 从Canary swaption这个仅有两个行权日期的简化版本出发，推导出解析定价方法后逐步推广。

支撑推理与假设：

• 利用swap rates分布与其间相关性，而非传统难以观测参数，实现了直接、以数据驱动的定价方法。

- 其理论假设基础为swap rates动态可用少量假设捕捉，以期进行半解析或解析定价。

---

2. Midcurve Swaptions （第1节）

核心内容：

• 介绍midcurve swaption的定义和定价框架。midcurve swaption的特殊性是在行权日和swap起始日间存在显著时间间隔。

- 表达midcurve swaption的价格为基于long swap和short swap两部分swap rates的相关加权组合，权重对应swap相关的年金比率。

公式要点：

• 通过年金概率测度 $\mathcal{A}$，将swaption价格以期望形式展开。

- 引入行权期内swap rates的联合分布和相应的copula积分实现定价。

• 解析地展示了换算为年金比率的随机变量处理过程，并提出了年金比率是否随机的假设对模型及计算的影响。

关键数据点：

• 关键变量包括$A(t,Ts,Te)$代表的swap年金，以及$R(t,Ts,Te)$为swap当期参考利率。

- 用到之前文献中的copula方法整合两个关键swap rates联合分布。

模型假设及处理：

• 主假设包括年金比率被视为确定性或接近确定性，以简化Jacobian和换算权重。

- 通过线性化近似可调节不确定年金比率的影响，保持模型的解析可计算性。

---

3. Swaptions with Relative Strikes（第2节）

核心内容：

• 传统swaption的行权价雖基于ATM基础调节，但行权价本身通常签订时即固定。

- 考察一种修改形式的swaption：行权价的基准ATM价固定时间$T{fix}$可以在行权日前，因此此种合同的行权价格本身为随机变量。

• 我们考虑以下两种情况：

- ATM价在行权时固定，与传统看涨/看跌期权一样，价格确定。
- ATM价提前固定（$T{fix} < Ts$），使得行权价格本身为随机，需用二元copula整合两个相关swap率的联合分布。

关键公式：

• 相关swap rates间的协方差推动了模型中swap率间的相关性（如定理3）。

- 通过该相关系数$\rho$，推导两个以Gaussian假设的swap rates间的关系；

• 在Gaussian假设下，swaption相对行权价价格可用Bachelier定价公式解析给出，

- 特别注意与$\sigmax = \sigmaz$情况下的简化条件，价格退化成确定性。

---

4. Canary Swaptions（第3节）

核心内容：

• Canary swaption是最简单的Bermudan swaption，有两个行权日期$T1 < T2$。

- 利用之前的相对行权价思想构造Canary swaption的价格表达式，包含在第二个swap年金测度$\mathcal{A}2$进行期望计算。

• 需要将第一个行权期权的价格从其自然测度$\mathcal{A}1$转移到$\mathcal{A}2$测度中，这一转变通过相应年金比率的确定性/凸性调整处理。

定价公式：

• 将待行权swaption价格拆解为最大值函数，涉及两个具有相关性的正态变量，

- 利用Gaussian联合分布和copula积分计算该最大值的数学期望，

• 明确涉及变量$X1$, $Z$的联合高斯分布，两个变量来自不同时间和不同swap期限测度。

相关性计算：

• 给出计算相关系数$\rho{X_1,Z}$的公式，基于各swaption隐含波动率和年金比率。

- 当forward rates完美相关时（corollary 1），该复杂模型简化成两正态变量最大值的情况，适用于快速计算与风险管理。

---

5. Bermudan Swaptions Pricing（第4节）

核心内容：

• 基于Canary swaption的分析推广到一般Bermudan swaption拥有多期行权的情形。

- 通过归纳计算（backward induction）构造Bermudan swaption定价：递归地计算每个行权日期的期望最大值。

• 量化描述了swap rates之间相关矩阵的构建，涉及很多个swap rates的交叉时间点以及对应的相关性计算。

- 具体给出了swap rate间相关性的表达式，联动关键年金比率和隐含波动率。

定价方法两大实做方向：

• 完美相关性假设（Theorem 7）：

- 假设所有forward rates间完美相关，降低计算复杂度，
- 该情况下Bermudan swaption价即为相关正态变量的最大值期望，
- 利用moment matching等技术给出定价方案。

• 数值格点法格型定价（Lattice Pricing，Theorem 8）：

- 类似Hagan LGM模型，定义对应的递归期望函数及其计算策略，
- 按行权日期倒序递归计算交换利率的条件期望和swaption期望，
- 该方法能较好考虑波动率微笑和非高斯效应，更接近市场实际。

市场对比（图2）：

• 模型与传统Hagan LGM模型对比，利用2025年真实市场数据，

- 发现纯moment matching模型偏低且需假设超高相关性才接近市场，

• 新格点模型(Annuity Lattice)表现出更优的市场拟合能力。

---

6. Stochastic Ratios of Annuities（第5节）

• 进一步考虑了年金比率的随机性对定价的影响，

- 依据前面提出的线性化与凸性调整理论（Theorem 2），

• 仅需对关键swap rates进行局部的凸性调节，即可较好捕捉年金随机带来的影响，

- 该策略简化了商业实现，减少了参数复杂度。

---

7. 结论（Conclusion）

• 论文提出的定价模型充分利用了swap rates的市场分布和相关性，解决了传统基于均值回复参数的模型标定难题。

- 通过替换人为难观测的参数，模型实现了更为透明和市场导向的定价机制。

• 该方法不依赖于产品特定的复杂校准，且计算框架简单，能够提升风险管理的效率和准确度。

- 实现上需要结合midcurve swaption、relative strike swaptions和Bermudan swaptions三类市场的协同，虽三市场均属复杂产品且受供需影响波动，但长期来看具备交易与风险管理潜力。

作者还表达了对合作团队和研究支持的感谢。

---

3. 图表深度解读

图1（第9页）

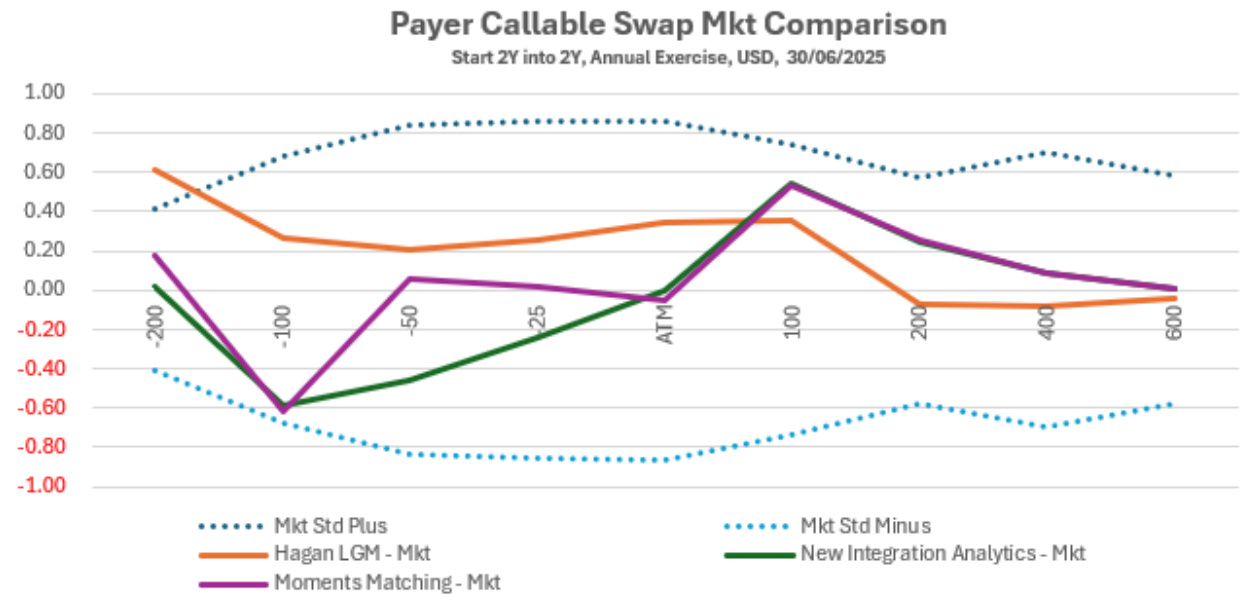
• 描述：展示了三种模型对Canary swaption的定价结果与市场共识的偏差。产品为2年后开始、可行权两次的payer类型callable swaption，按连续行权频率计。

- 曲线及含义：
- 虚线表示市场报价的标准差区间（正负一倍标准差）。
- 橙色线为经典Hagan LGM模型差价。
- 绿色线为本文提出的半解析积分模型差价。
- 紫色线为基于moment matching的近似估算模型差价。

• 趋势解读：

- Hagan LGM在大部分行权价上表现出轻微正差价（高估价）。
- 积分模型和moment matching总体接近市场，其中积分模型波动较平缓，moment matching对极端行权价反应灵敏。
- 两新模型表现较好，尤其在接近ATM区域，显示其解析定价模型的有效性和市场适应性。

• 联系文本：该图验证了Canary swaption半解析定价模型的可行性，且支持用相关性直接估计价格的假设。

- 潜在局限：该比较基于特定市场数据，供需因素未量化；模型对极端尾部风险考虑不足。

---

图2（第13页）

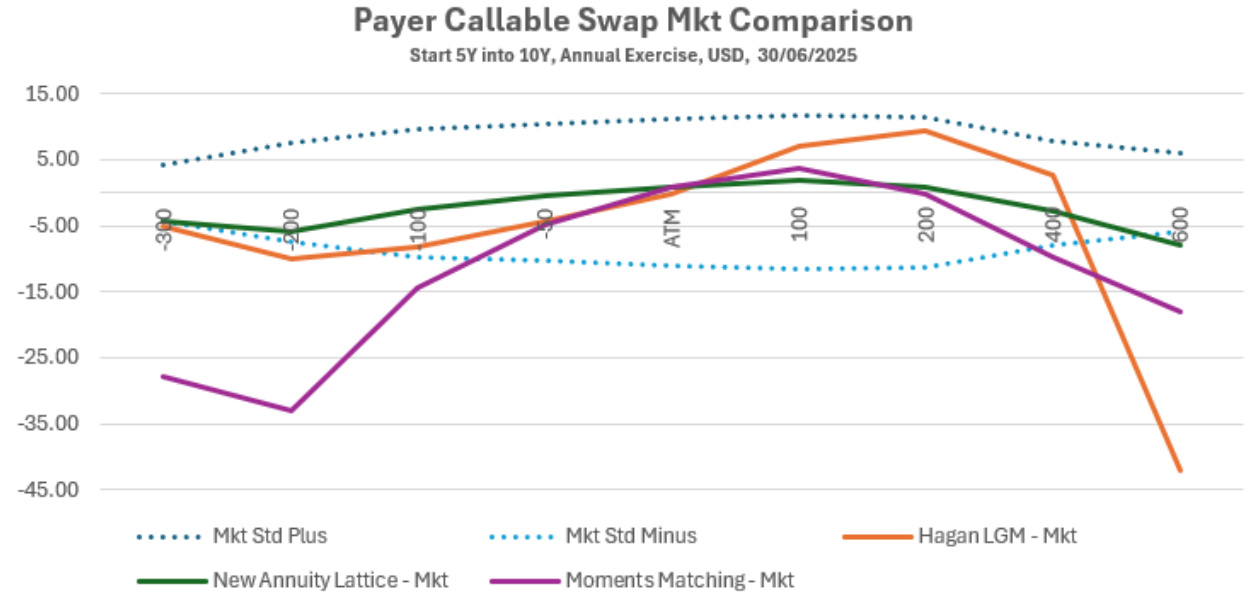
• 描述：展示不同模型对长期（5年后开始，10年期限，年行权）Bermudan swaption价格与市场共识的偏离。

- 曲线：
- 虚线为市场价格上下波动范围。
- 橙色为Hagan LGM模型。
- 绿色为报告中提出的带年金调整的Lattice模型。
- 紫色为moment matching技术模型。

• 趋势：

- Hagan LGM对部分行权价高估（苛刻行权价明显高估）。
- moment matching模型在多数点显著低估，接近市场低端6-8个基点。
- 新Lattice模型较稳定，整体更接近市场中心值，表现出较好的拟合能力。

• 联系文本：

- 反映复杂Bermudan swaption需高度相关矩阵和较丰富波动性结构，
- 作者指出moment matching结果低估可能是相关设置未完全匹配市场。
- Lattice模型有效集成多期行权结构，提供实用方案。

• 局限与提醒：

- 高度相关的假设在现实中可能并不总适用。
- 市场供需和微笑效应未完全捕捉。

---

4. 估值分析

• 估值方法：

- 采用基于swap rates年金概率测度的半解析公式。
- 通过copula集成理解多个swap rate的联合行为。
- 在Gaussian假设下，应用Bachelier模型进行简单解析定价。
- 递归法和格点（Lattice）方法：通过向后迭代精确处理多时间行权结构，实现对Bermudan swaption的动态定价。
- Moment matching方法在假设正态分布及相关性的基础上，通过匹配前几阶矩估计最大值的分布。

• 主要输入与假设：

- Swap rates及其forward starting swap的隐含波动率。
- 利用交易市场midcurve swaptions和CMS spread推断相关性矩阵。
- 年金比率视为确定性或带可控凸性调整。
- Gaussian假设确保积分可微分及可计算。

• 估值范围和敏感性分析：

- 估值显著依赖相关性水平，特别是为提高近似估值准确性，将相关性调整至极高水平（近100%）。
- 年金比率的随机性通过凸性调整影响估值，体现对未来利率路径的敏感度。
- 通过比较不同模型和市场价格，体现模型在波动率笑面和相关结构下的适应能力。

---

5. 风险因素评估

报告所识别主要风险及潜在影响包括：

• 相关性估计风险：

- 相关矩阵的估计对最终定价有重大影响，
- 如相关性估计偏差，将导致定价系统性偏差。

• 波动率笑面和波动率动态的风险：

- 以Gaussian和Bachelier为假设的模型，可能无法充分捕捉动态微笑效应。

• 年金比率随机性风险：

- 如果年金比率的随机性未充分校正，可能导致模型估值不准确。

• 市场供需和流动性风险：

- 报告提及midcurve、Bermudan和relative strike swaptions市场均缺乏充分流动性，导致价格受限于非完全无套利因素。

• 模型假设风险：

- 多处模型假设（如均值回复参数摒弃、Gaussian分布、无产品特定校准）可能在极端市场环境中失效。

对于大部分风险，报告通过理论上的凸性调整、相关性调节以及copula积分模拟提供了缓解方法，但未详细量化事件发生概率。

---

6. 批判性视角与细微差别

• 优点：

- 创新性地替换难以估计的均值回复参数，改为可观测相关系数，
- 兼顾了模型简化与维持真实性的平衡，
- 提供一整套理论解析与实务计算方法，从半解析到数值格点定价。

• 潜在局限与假设质疑：

- Gaussian分布假设和Bachelier定价模型虽简洁，但对极端风险或波动率笑面处理有限。
- 年金比率随机性以线性化处理或凸性调整简化，可能低估其对价格动力的非线性影响。
- 相关性估计仰赖历史数据或隐含市场数据，对于市场瞬变和异常情况缺乏快速响应能力。
- 量化研究侧重理论推导和静态市场条件，缺少对动态利率环境下的长期性能测试。
- 报告提出的模型须同时与三个相对复杂的市场（Bermudan、midcurve、relative strike swaptions）同步调整，现实中执行复杂。

• 内在矛盾或待注意点：

- 报告中moment matching估值结果偏低，需要依赖接近100%的相关性设定才能接近市场定价，显示模型对相关性的敏感性极高且对实际市场条件有一定偏离。
- 对于深度实战应用，模型或需加入更多非高斯跳跃风险或波动率结构调整。

---

7. 结论性综合

本文提出了一种基于swap rates分布与相关性、无需基于传统均值回复等隐含参数校准的Bermudan swaption定价模型。其创新之处在于通过numeraire转移简化定价过程，实现多期限利率期权的统一半解析方法，为实际衍生品交易和风险管理提供了更为透明高效的工具。

具体贡献如下：

• 通过年金概率测度和copula积分技术整合midcurve swaption和Bermudan swaption的定价，创新地将相对行权价swaption作为连接桥梁。

- 在Canary swaption案例中，详细推导解析定价及其高斯近似，成功应用后推广到多期Bermudan swaption，提出了基于相关系数和波动率矩阵的递归期望求解策略。

• 结合Gaussian假设和Lattice差价法，能灵活处理波动率笑面、相关性结构和年金随机性，满足复杂实务需求。

- 市场实证显示，该方法对比经典Hagan LGM模型，在多个市场环境和执行价格点表现更接近市场价格，特别是在风险管理框架下提供了更快捷和准确的方案。

• 模型对相关性参数极度敏感，且需求对多个相关市场同步考量，表明在操作应用中仍需谨慎对待市场流动性与模型调整策略。

综上，该报告为衍生品定价领域提供了理论基础扎实且具较强应用潜力的替代方案，尤其适用于需要避免繁复、难以校准参数的Bermudan swaption定价和风险管理场景。

---

参考：

- 本分析严格基于报告文本内容及其数学公式、图表，引用页面详见标注。本解析涵盖所有主要章节及两张关键图表，并对模型假设、推导逻辑、定量表现进行了详尽解读。[page::0-14]

报告