研究背景与模型设计 [page::3][page::4]

• 交易量与波动率一般正相关，但考虑交易量的正负分量（基于日内收益）可能对已实现波动率有非对称影响。

- 提出两类模型：模型一基于日内收益分解交易量正负分量(HAR-AV1、HARL-AV1等)，模型二基于日度收益分解交易量正负分量(HAR-AV2、HARL-AV2等)。

• 引入杠杆效应变量即负收益对波动率的放大作用，完善模型。

数据与描述性统计 [page::5][page::6]

| 变量 | Mean | Median | Max | Min | SD | Kurtosis |
|-------|-------|---------|-------|-------|-------|----------|
| 已实现波动率(RVt) | 0.218 | 0.109 | 27.47 | 0.008 | 0.688 | 745.1 |
| 正收益波动率(RV+) | 0.107 | 0.049 | 26.76 | 0.003 | 0.442 | 2634 |
| 负收益波动率(RV-) | 0.111 | 0.047 | 20.14 | 0.002 | 0.446 | 983.2 |
| 交易量(SV) | 47173 | 42983 | 415306 | 3788 | 30731 | 16.45 |

• 变量间存在显著相关性，交易量与波动率正相关，且交易量正负分量均有影响。

回归及实证结果 [page::7]

• 基准HAR模型显示交易量正向显著影响波动率。

- 引入不对称交易量变量后，基于日内负收益的交易量对波动率影响显著正向，基于日内正收益的影响负向或无显著性，证实非对称效应存在。

• 杠杆效应变量显著，负收益增强波动率。

- 日内收益非对称交易量变量模型相较基于日度收益的模型拟合更优。

样本外预测性能比较 [page::8][page::9][page::10][page::11]

• 使用滚动窗口回归，基于多样标准（HMSE、HMAE、QLIKE）评估预测误差。

- 非对称交易量变量模型(如HAR-AV1, HARL-AV1, RSVL-AV1)整体优于对称变量模型(HAR-SV等)。

• 基于日内收益的不对称交易量变量模型优于基于日度收益模型。

- MCS检验进一步确认引入不对称变量和杠杆变量显著提升预测性能。

结论与展望 [page::13]

• 交易量对已实现波动率存在明显的非对称效应，特别是基于负日内收益的交易量更显著地推动波动率增大。

- 考虑不对称交易量变量明显提升波动率建模和预测的精度，基于高频日内信息尤为有效。

• 未来研究可以考虑将该模型扩展至周度或月度频率及应用于能源商品等多种资产波动率预测。

交易量对波动率的非对称效应——“学海拾珠”系列之一百六十详尽分析报告

---

一、元数据与概览

• 报告标题：交易量对波动率的非对称效应——“学海拾珠”系列之一百六十

- 作者与机构：
- 作者之一：卢昱杉，执业证书号 S0010522110001，邮箱：luoyushan@hazq.com
- 作者之二：严佳炜，执业证书号 S0010520070001，邮箱：yanjw@hazq.com
- 发布机构：华安证券研究所

• 发布日期：2023年9月27日

- 研究主题：探讨交易量对已实现波动率的非对称影响，通过引入改进的波动率模型，特别在已实现波动率的预测中，评估正负收益对应的交易量分量对波动率的不同作用。

• 核心论点：

- 交易量对已实现波动率具有显著的非对称影响，其中负收益驱动的交易量对波动率的提高作用更为显著。
- 引入非对称交易量变量能够有效提升已实现波动率的预测精度。
- 基于日内收益构建的非对称交易量变量模型优于基于日度收益的对称及非对称模型。

• 风险提示：研究结论仅基于历史数据与国外文献总结，不构成投资建议。

该报告立足于学术文献 Daiki Maki 的文章《Asymmetric effect of trading volume on realized volatility》，结合华安证券研究所实证分析，应用高频数据，体现了交易量在波动率建模中的最新进展和改进尝试。[page::0,3,14]

---

二、逐节深度解读

1. 简介与研究背景

报告开篇强调交易量与波动率在市场行为研究中的关键角色。波动率采用已实现波动率的定义，即日内高频收益的平方和，这一估计方法已有广泛采纳，因其可显著提高波动率估计的准确性。已有文献指出交易量与已实现波动率之间存在正相关关系，但这种关系对波动率的不同成分（连续或不连续）有不同影响。

特别，报告关注波动率的非对称性质，引用杠杆效应及RSV模型对正负收益波动率影响的区分。基于这一理论，本文提出创新性地分解交易量为正收益和负收益对应的部分，进一步验证交易量的非对称交易对已实现波动率的影响差异。[page::3]

2. 模型构建：引入不对称交易量的HAR模型

• 模型基础：

- 已实现波动率计算为日内分段收益率平方和 \(RVt = \sum{j=1}^n r{t,j}^2\)。
- HAR（Heterogeneous AutoRegressive）模型捕捉日、周、月三个尺度的波动率信息，模型形式为对数已实现波动率的线性组合，自变量包含今日、5日均值和22日均值的对数已实现波动率，适用于捕捉波动率的长记忆效应，并缓解极值影响。

• 引入交易量变量：

- 交易量以日总交易量 \(S Vt\) 对数形式加入模型，标准变量假设为正相关波动率。
- 进一步将交易量分解为日内收益为正和为负的交易量分量 \(AV{1t}^+, AV{1t}^-\)（模型一，基于高频数据）及基于日度收益的分量变量 \(AV{2t}^+, AV{2t}^-\)（模型二）。预计负收益对应的交易量分量对波动率的影响更大。

• 杠杆效应与扩展：

- 结合杠杆效应，即负收益对波动率产生正向冲击，进一步将其作为指标引入模型（HARL-SV、HARL-AV1、HARL-AV2）。
- 采用Patton和Sheppard(2015)的RSV模型框架，引入正、负半方差概念，将交易量和交易量的非对称分量嵌入，以捕捉更复杂收益与波动的非对称结构。

该部分充分展示了从理论到模型设计的逻辑和创新点，即通过交易量的非对称分解结合波动率建模，提高对市场隐含动态波动的映射能力。[page::4,5]

3. 实证数据及样本介绍

• 数据采用日本东证期货的5分钟高频数据，覆盖2001-2021年两十年区间，拥有丰富的高频市场信息。

- 选择了9个模型，其中包括3个对称交易量变量模型和6个非对称交易量变量模型。

• 关键变量的描述性统计表明已实现波动率及其正负分量，交易量及其非对称分量均存在高波动性和明显偏态，偏度及峰度较高，反应金融市场特征的尖峰厚尾。

- 相关矩阵显示，各波动率指标和交易量分量高度正相关，非对称分量之间也展现复杂的相互关系，且杠杆效应指标与负收益变量正相关体现预期的市场反应机制。[page::6]

4. 回归分析与非对称效应检验

• 回归结果表明，基线模型中交易量对已实现波动率正向影响显著，但系数较小，显示对称交易量解释力有限。

- 非对称模型中，基于日内负收益交易量的回归系数均显著为正，而基于正收益交易量系数为负或不显著，验证了交易量的非对称效应。

• 引入杠杆效应使得负收益与波动率的关联更加显著，加深了模型理论的合理性。

- 日内收益构建的非对称交易量变量模型优于日度收益变量模型，解释力（调整后的 \(R^2\)）提升明确。

• RSV模型和HAR模型均表现出对非对称交易量的敏感性和优越性，进一步增强实证结论的稳健性。[page::6,7]

5. 样本外预测与滚动窗口分析

• 利用滚动回归技术，采用不同样本窗口（包含完整东证期货交易周期调整），针对1、5、22天不同预测期，动态估计交易量非对称参数。

- 滚动估计图表显示负收益交易量系数始终为正且稳定，正收益系数往往负向且较小，体现非对称效应时间演变的规律性。

• 预测效果采用HMSE、HMAE、QLIKE三种不同的损失函数，涵盖误差的均方和绝对值，保证结果全面且鲁棒。

- 采用Diebold-Mariano检验比较不同模型预测优劣，非对称交易量变量模型（特别HAR-AV1）大幅优于对称模型和基于日度收益的非对称模型，均在1%显著水平上显著提升预测性能。

• 纳入杠杆效应非对称变量也能提升预测性能，但基于日内收益非对称交易量作用更为明显，表明高频数据中交易量分解能提供更精细的波动率预测信息。[page::8,9,10]

6. 多模型比较与MCS检验

• 利用模型置信集（MCS）检验，针对9个模型在不同样本尺寸（1000、2000、3000）和不同时点的预测表现，输出包括Tmax和TR检验统计量。

- 结果表明，包含杠杆效应（HARL系列）和RSV改良的模型普遍拥有较高的p值，表现为在模型组中被认可的可能性高。

• 特别是非对称交易量变量（基于日内收益）相关模型在MCS检验中显示出更强预测力。

- TR检验能够更灵敏地区分模型间的预测效能，强调了使用非对称交易量变量的优势。

• 综上，MCS检测支持了本文提出的非对称交易量分量模型在提升已实现波动率预测中的实证权威性与预测准确性。[page::11,12,13]

7. 讨论与总结

• 总结部分明确指出，常规波动率模型忽略交易量的非对称效应存在缺陷，本研究通过溯源高频收益的交易量正负分解提高波动率建模精度。

- 练习性地引入杠杆效应和RSV模型，进一步丰富了理论模型，验证了其显著效果。

• 研究实证结果显示非对称交易量—特别是基于日内负收益的交易量—对未来波动率有显著且正向的影响。

- 非对称交易量变量模型优于对称交易量模型，并且在样本外预测中表现更佳。

• 后续研究方向建议扩大数据尺度（周、月度）及不同市场领域（能源、商品）应用，同时探讨交易量非对称性对波动率溢出效应的影响。

- 该研究对于金融市场风险管理、波动率预测模型构建提供了重要启示，彰显了高频数据和非对称变量在现代资产定价中的价值。[page::13]

---

三、图表深度解读

图表1-3：非对称数据描述统计与相关矩阵

• 内容：完整展现各变量（包括已实现波动率总量及正负分量、总交易量与分量、杠杆变量等）的均值、中位数、极值、波动率、偏度和峰度；及变量之间相关系数，分别基于水平数据与对数变换数据给出。

- 关键观察：
- 已实现波动率及其正负分量均呈高度正偏态与峰态，显示金融市场波动剧烈时段的极端表现。
- 正负收益交易量分量均与总体波动率高度正相关。
- 负收益相关变量与波动率表现更强关联，支持理论假设中波动率的负收益杠杆效应和非对称影响。

• 文本联系：支持基本假设中交易量对波动率的非对称影响，变量相关性映证理论基础。[page::6]

图表4：回归结果表

• 内容：涵盖所有9个模型的核心回归参数估计，系数统计显著性标注及调整后 \(R^2\)。

- 解读：
- 对称交易量变量（HAR-SV）相关系数虽显著但幅度较小。
- 非对称交易量变量β1（正收益分量）多数为负，β2（负收益分量）为正且显著，强化非对称效应观点。
- 引入杠杆效应系数γ显著为正说明负收益提升波动率，验证经典杠杆效应。
- 调整后 \(R^2\) 从0.514提升至0.546，显示模型拟合质量明显提高。

• 意义：实证验证非对称交易量分量的必要性及有效性。[page::7]

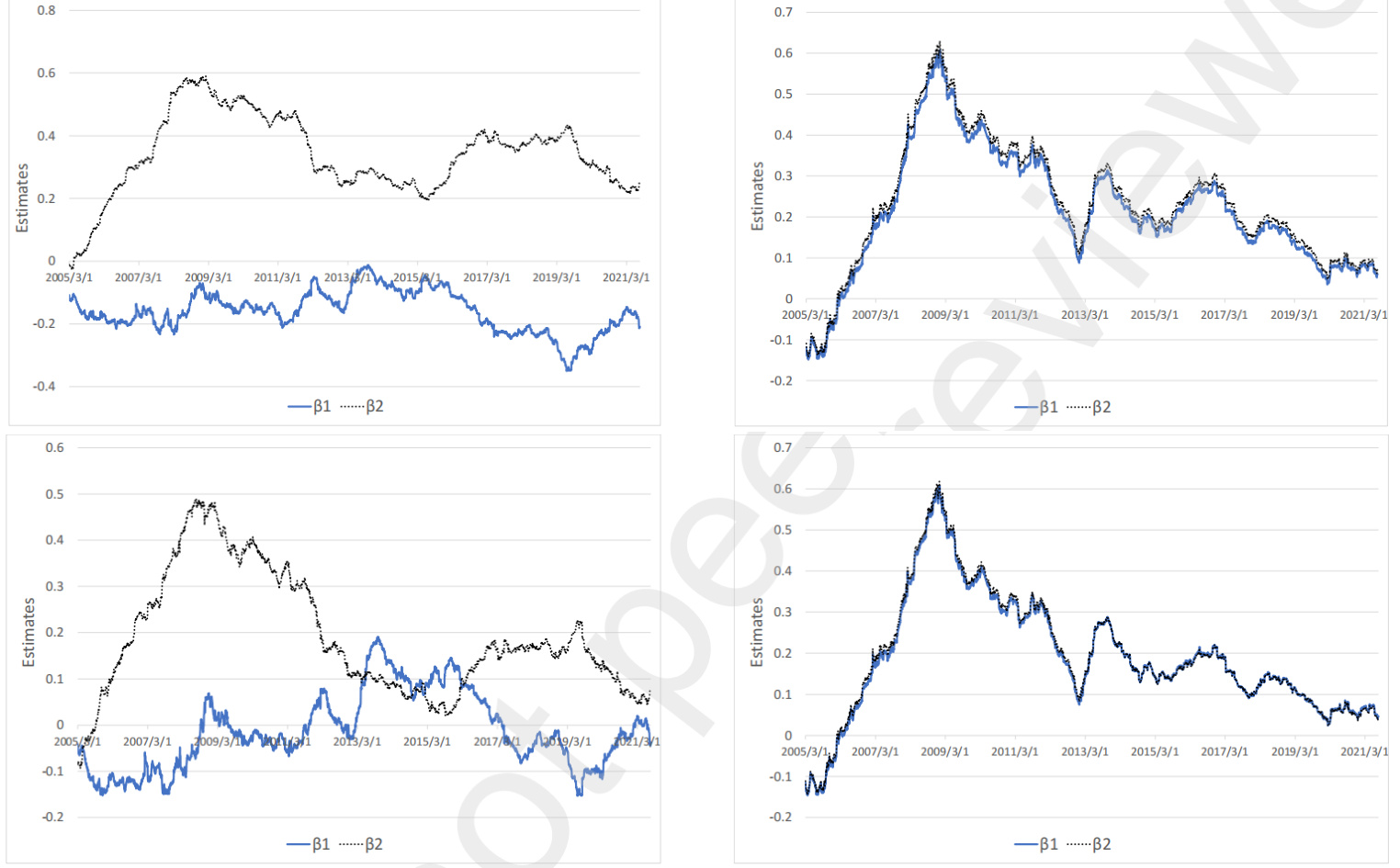
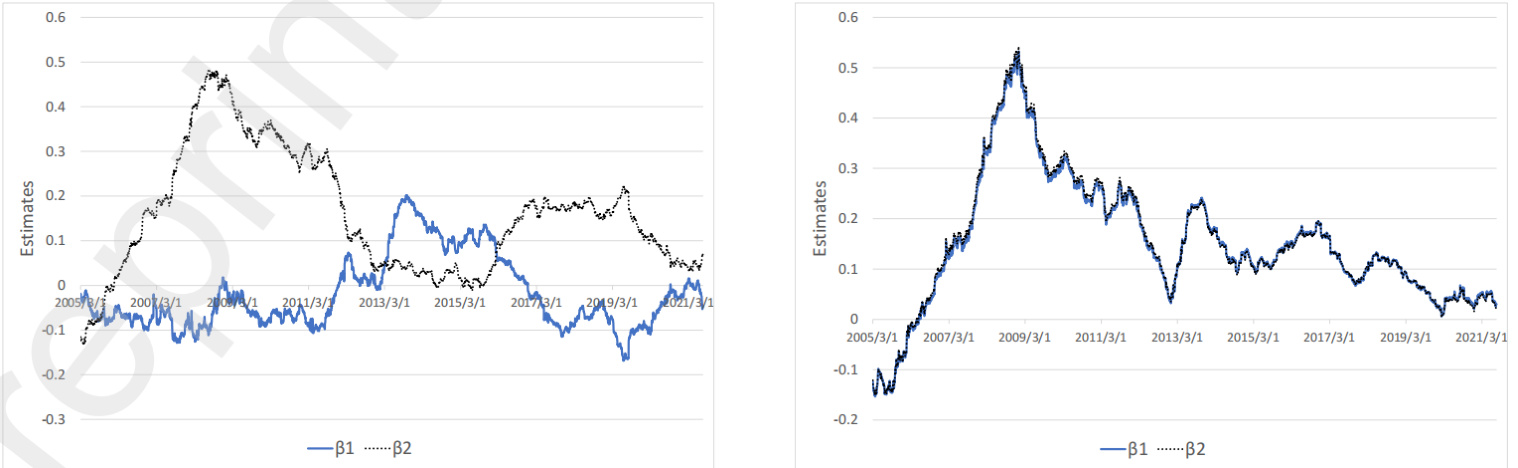
图表5：样本外滚动窗口估计图

• 内容：不同样本窗口期下模型中β1和β2的滚动时间序列估计。

- 观察：
- β2（负收益分量）持续为正且显著，波动相对平稳。
- β1（正收益分量）参数回归值多数为负，且波动较大。
- 不同模型间非对称效应显著，基于日内收益的模型差异更明显。

• 联系：揭示非对称交易量效应的稳定性和时间序列动态特征，进一步支持报告结论。[page::8]

图表6：Diebold-Mariano检验统计量

• 内容：比较不同模型预测已实现波动率的差异显著性，涵盖多样损失函数（HMSE、HMAE、QLIKE）和不同样本规模。

- 解读：
- 非对称交易量模型显著优于对称模型，均达到1%显著性水平。
- 基于日内收益的非对称交易量变量模型总体预测效果显著好于基于日度收益的模型。
- 杠杆效应引入后，模型预测性能进一步提升，但日内非对称变量依旧表现最佳。

• 意义：证明改良模型在实际应用中具备更高的预测准确性和实用价值。[page::10]

图表7：模型置信集（MCS）检验统计量

• 内容：针对9模型的整体预测优劣判定，给出p值及检验统计，涵盖短、中、长期预测期。

- 分析：
- 包含杠杆效应和RSV变量的模型获得最高p值，长期保持优势地位。
- 非对称交易量基于日内收益构建的模型显著位居优胜模型集，证明其优异性。

• 关系：强调了交易量非对称性的模型改进不仅统计显著且综合表现更佳，具有普适预测稳定性。[page::11,12,13]

---

四、估值分析

本报告属于学术研究分析，主要聚焦交易量非对称对波动率建模的改善，并无涉及公司估值、价格目标或投资评级等内容，因此无估值分析章节。

---

五、风险因素评估

• 风险提示：

- 结论基于历史高频数据及海外文献总结，具有一定时效性和区域特性，难以直接推广至其他市场或时间段。
- 高频数据噪声及结构变化可能影响模型稳定性。
- 杠杆效应及非对称效应的准确捕捉依赖于选取的收益划分和统计方法的假设合理性，存在模型误设风险。

• 缓解：报告建议后续研究使用不同数据频率及市场验证，增强模型稳健性。

---

六、批判性视角与细微差别

• 报告整体论述严密，理论推导与实证分析相辅相成，但存在以下需要注意的细节：

- 杠杆效应的引入虽提升模型表现，但对涨跌因素的影响机制复杂，可能与日度和日内收益定义有关，仍需进一步理论解构。
- 非对称交易量对正负收益的区分建立在指示函数上，模型中截断点的合理性及敏感性未作充分探索。
- 样本期间覆盖日本市场，结构性特点可能限制结论在其他市场的普适性。
- 回归模型基于对数线性假设，存在未检验的非线性或时变参数风险。

• 该研究为学术先导探索，实际应用时需结合实际市场特征和宏观环境加以调校。

---

七、结论性综合

本报告系统地探讨了交易量对已实现波动率的非对称效应，创新性地将交易量划分为基于日内及日度收益正负分量，结合高频数据和先进波动率建模技术（HAR和RSV模型），揭示了负收益产生的交易量对波动率提升作用更为显著的事实。实证结果多维度验证非对称交易量模型在拟合及预测已实现波动率方面均优于传统对称模型，尤其是基于日内收益的非对称变量模型显示出更强的解释和预测能力。

通过描述性统计、回归分析、滚动窗口估计、较严厉的预测表现测试（Diebold-Mariano检验）、及模型置信集MCS检验，报告全面论证了非对称交易量变量在捕捉市场波动动态中的关键价值。引入杠杆效应作为补充，进一步提升模型完备性。

从图表来看：

• 描述统计揭示交易量和波动率指标的极端波动特征和分量差异；

- 相关矩阵显示正负收益和交易量分量的多重非线性关联；

• 回归结果明确展示负收益对应的交易量系数显著为正，正收益系数为负，支持非对称效应假设；

- 样本外滚动回归图示和DM检验强化了日内非对称变量模型的预测优势；

• MCS检验进一步确认综合模型框架的统计显著性和预测稳定性。

本报告显示：在已实现波动率的建模和预测中，忽略交易量的非对称性将导致模型偏误和预测力下降，充分考虑负收益驱动的交易量分量及相关非对称变量对于风险管理和量化投资策略设计至关重要。

总结而言，非对称交易量效应的引入丰富了波动率建模的理论与实证视角，为金融市场波动动态的理解与预测提供了新颖且有效的路径，为投资者和学者均提供了有价值的参考框架和工具。[page::0,3,4,5,6,7,8,9,10,11,12,13]

---

附：重要图表示例

• 图表 滚动测试结果（样本窗口期为 ）

• 图表 样本外预测检验示意及统计量

---

免责声明

本报告基于公开信息编制，仅供参考，不构成任何投资建议。投资需谨慎，风险自担。[page::14,15]

报告