研究背景与动机 [page::0][page::1]

• 结合均场博弈理论与二项树模型解决股票价格形成均衡问题。

- 代理人服从指数效用或递归型指数效用，面临带有公共和个体风险的随机负债与赋予。

• 外部订单流考虑了大金融机构或其他市场参与者的影响。

基础模型设定与优化问题 [page::2][page::3][page::5]

• 股票价格路径限制于重组的二项树，转移概率依赖于当前价格与宏观状态变量。

- 代理人选择自融资交易策略，最大化终端财富的期望指数效用，终端收益受随机负债影响。

• 优化解的显式表达式通过递归价值函数构造，且代理人风险厌恶参数影响最优持仓。

均场均衡与转移概率刻画 [page::7][page::8]

• 均衡条件为所有代理人最优持仓的总和匹配市场外部订单流。

- 唯一均衡存在，均衡转移概率公式显式包含代理人异质性和平均风险厌恶。

• 在大样本极限下，需求匹配的均方误差以1/样本量速率收敛。

经济含义与扩展到递归效用模型 [page::9][page::10][page::15]

• 负债与增量赋予对风险溢价有决定性影响：逆周期负债增加风险溢价，正向波动则可能导致负风险溢价。

- 递归效用体系引入现金消费，转移概率依赖价格路径历史，能更精细刻画动态效用行为。

• 多群体均衡允许不同效用形式代理人混合存在，转移概率由加权均衡条件唯一确定。

数值分析与实证启示 [page::18][page::19][page::20][page::22][page::23][page::24]

• 以具体参数模拟无路径依赖情形，展示均衡价格分布相较风险中性分布具有显著偏离。

- 不同负债信号（增减对股价的敏感性）对应风险溢价正负不同，支持理论预期。

• 外部订单流正负分别造成均衡价格分布右偏和左偏，验证均衡转移概率的经济合理性。

- 递归效用比率参数控制风险溢价大小，影响偏离风险中性分布的幅度及时效。

• 异质性波动率对交易量影响显著，但对风险溢价影响甚微，实现风险溢价与交易量的解耦。

量化模型贡献与未来方向 [page::24]

• 明确证明指数效用和递归效用代理人下均衡存在唯一性，以及均衡转移概率显式表达式。

- 方案兼容多资产、多群体扩展，实用性高于连续时间qg-BSDE框架。

• 未来可拓展至一般多项树、多资产场景，以及其他效用类型（如幂效用）等更复杂设定。

金融研究报告详尽分析报告——《Mean-Field Price Formation on Trees》

---

1. 元数据与概览

报告标题： Mean-Field Price Formation on Trees
作者： Masaaki Fujii
首次版本日期： 2025年10月13日
研究主题： 本文聚焦于股票价格形成的均衡问题，结合均场游戏理论（Mean-Field Game, MFG）和经典的二叉树价格框架，致力于构建基于多智能体行为的均衡价格动力学模型。研究涉及时序金融资产动态、代理人效用优化以及多因素风险对价格变动的影响。

核心论点概述：

• 通过将价格演化路径限制在二叉树结构，本文建立了一个明确的均场均衡模型，并证明在代理人具有指数效用及递归效用（指数型）时存在唯一均衡。

- 引入外生未对冲的公共与个体风险因素，考察其对代理人终端负债与持续增量收益的影响，体现市场真实多样风险特征。

• 给出算法明确的均衡转移概率公式，便于数值求解和政策模拟。

- 通过数值例证说明不同市场环境与代理人特征参数对价格分布的影响，揭示均衡价格形成机制。

报告强调了结合经典金融定价理论和现代均场理论的创新，突破了传统模型在处理非连续交易策略和直接财富效用函数上的限制，为市场均衡价格动态研究提供了新的理论和实用工具。

---

2. 逐节深度解读

2.1 引言

• 主要内容：

介绍均场游戏理论的起源，历程及其在金融市场价形成中的潜在应用。文献回顾了MFG理论由Lasry & Lions与Huang等人最初建立，随后转向概率方法（FBSDE）进行扩展，强调其能将多智能体动态博弈降解为优化与固定点问题，并说明金融和能源市场是典型的对称代理人均场应用场景。

• 推理依据与背景：

引用众多最新文献指出MFG在经济增长、财富分布以及动态需求管理中的应用广泛，且已有学者将MFG应用于随机电价、碳排放交易、可再生能源证书定价等，奠定了其应用基础。

---

2.2 经典二叉树框架下的指数效用均场优化（第2章）

2.2.1 模型设定与概率空间构造（第2.1节）

• 论点总结：

构建一个多智能体模型，时间离散，均依赖于有序时间序列区间的二叉树股价过程\( Sn \)和公共因子\( Yn \)；每个代理人拥有个体性质与私有噪声\( Zn^i \)，自由选择股票持仓量实现财富最大化。

• 关键假设：

1. 股票价格涨跌幅\(\widetilde{u},\widetilde{d}\)固定且满足无套利条件 \(0 < \widetilde{d} < e^{r\Delta} < \widetilde{u}\)；
2. 公共因子与个体因子均为马尔科夫过程；
3. 股价路径受限在重组的二叉树，实现有限状态空间，方便计算；
4. 成员间独立同分布（iid）、风险厌恶参数、初始财富在区间内有界。

• 模型架构解析：

联合概率空间使用无限乘积形式，反映独立性假设。股票价格由转移概率函数\(pn(s,y)\)控制，依赖于当前股票价格和公共因子，满足风险中性概率严格落在(0,1)区间保证市场无套利。

2.2.2 代理人单体投资问题（第2.2节）

• 目标函数：

代理人采用指数效用函数最大化期末财富扣除随机负债（终端负债函数\( F(SN,YN,ZN^i) \)），优化持仓策略\( \phin^i \)。

• 关键经济解释：

终端负债建模了依赖市场价格及其他共性和个体风险的非可交易风险（如其他业务收益或衍生品负债）。代理人视为价格接受者，不影响价格动态。

2.2.3 优化问题求解（第2.3节）

• 结果归纳：

引理与定理证明代理人最优持仓策略存在且唯一，呈显式形式，依赖于转移概率、风险厌恶系数与未来价值函数\( Vn \)。采用动态规划与向后归纳计算价值函数\( Vn \)，将最终效用函数转化为可递推计算形式。

• 数学表达：

最优持仓公式含对数转化转移概率和价值函数比值，体现对未来市场状态和风险厌恶的权衡。重要的是这一状态依赖策略形式允许数值计算。

2.2.4 均场均衡存在性与转移概率求解（第2.4节）

• 均衡定义：

市场均衡意味着全体代理人的平均持仓量与外部订单流\( Ln(s,y) \)相匹配，实现供需平衡。

• 主要定理：

唯一均衡存在且转移概率可通过均衡条件倒推求出，体现一种确定性映射关系。进一步证明大数定律下均衡的代理人平均策略收敛速率为\( 1/Np \)阶，保证均衡稳定性和实际适用性。

• 均衡概率公式：

转移概率依赖于风险规避系数的倒数均值、对数价值比值的加权期望以及净外部订单流，阐释均衡价格风险溢价由市场参与者整体风险偏好和负债结构决定。

2.2.5 经济含义与风险溢价分析（第2.5节）

• 风险溢价来源：

价格偏离风险中性概率取决于负债对股价的敏感度。负债大小随股价下降时，价格上升的概率\(p > p^{\mathbb{Q}}\)产生正风险溢价。反之，如果负债与股价同向变动，可能出现负风险溢价。

• 交易量解释：

非零的个体异质性（如\(Zn^i\)分布）是市场交易的根源，异质性越大，交易量越大。无个体异质性时，交易量趋近于零，市场无交叉交易。

• 外部订单流影响：

外部大户的订单流\( L > 0 \)提升供给，迫使普通代理人承担更大持仓风险，要求更高风险溢价，平衡供需，保证市场均衡。

---

2.3 递归效用拓展与路径依赖（第3章）

2.3.1 模型拓展设定（第3.1节）

• 扩展关键点：

允许收益和负债具有路径依赖，股价转移概率须随历史路径调整，非马尔科夫动态。引入现金消费决策及递归效用，涵盖时间非分离效用，更符合实际决策行为。

• 状态描述及随机变量：

新增风险厌恶参数\(\zetai\)、消费折现率\(\deltai\)、相对重要性参数\(\psii\)，并用向量\(\varrhoi\)表示。扩展股票价格及公共因子的路径空间描述。

2.3.2 递归效用下代理人优化问题（第3.2节）

• 财富动态及效用定义：

代理人财富根据消费、持股和增量收益动态调整。效用通过递归公式定义，体现消费与未来效用之间权衡，标准时间可分离效用为特例。

• 最优策略特征：

证明存在唯一适应性最优持仓和消费策略，策略表达依赖于新的状态函数与乘法因子\(\etan^i\)，并通过递归关系计算\( Vn \)。策略分解为持仓优化和消费优化两个独立子问题，分别求解。

2.3.3 均场均衡及风险溢价表现（第3.3节）

• 均衡定义升级：

均衡供应需求的匹配程度与路径相关，转移概率函数\( pn(\mathbf{s}, y) \)依赖路径。存在唯一均衡且相应概率表达式与之前类似，额外乘以路径相关因子。

• 经济含义深化：

风险溢价不单由终端负债决定，当前增量收益、消费偏好参数等也有重要影响，且相对参数比值\( \psii / \zetai \)决定风险溢价在时间上的分布特征。

• 市场异质性影响：

异质性（尤其是个体风险参数和私有因素）决定市场交易量规模，\(Zn^i\)波动加强市场活跃度，但不必然影响风险溢价大小。

2.3.4 多群体均衡问题（第3.4节）

• 多群体结构分析：

允许多个异质代理群体参与市场，群体间持仓策略均衡地通过群体权重加权求和，实现整体市场均衡。

• 计算便捷性：

即使群体间效用函数不同，均衡转移概率仍有显式解，降低多群体均衡计算难度。

---

2.4 数值实验分析（第4章）

2.4.1 无路径依赖指数效用模型数值分析（第4.1节）

• 模型与参数设置：

采用参数表1中定义的各类金融参数，针对单维度\(Yn\)、\(Zn^i\)及股票价格简化为二叉树过程，风险厌恶参数\(\gammai\)离散均匀分布。

• 主要负债函数形式（4.1）与结果：

\(F(SN,YN,ZN^i) = C - 3 SN YN ZN^i\)，负债随股价下降。

• 图表深度解析：

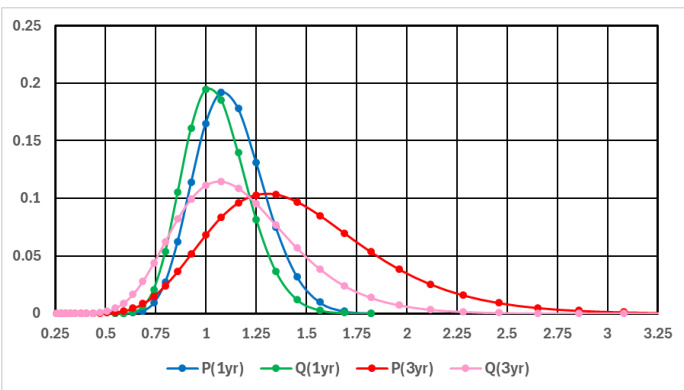
- 图1 显示1年和3年期的边际价格分布在均衡概率\(P\)下较风险中性概率\(Q\)更偏右（正风险溢价）；
- 图2 演示按公共因子\(Y\)分层的条件价格分布，\(Y\)高时风险溢价更明显；
- 图3 预期股价在均衡概率下长期高于风险中性期望，表明正风险溢价体现；
- 图4 显示随着时间推进，均衡市场交易量（位置标准差）递增，表明投资者交易活跃度增加。

• 相反负债形式（4.2）效果（图5至图8）：

将负债改为 \(F = C + 3 SN YN ZN^i\)，则风险溢价转负，价格分布左移，交易量变化适中，呼应理论分析。

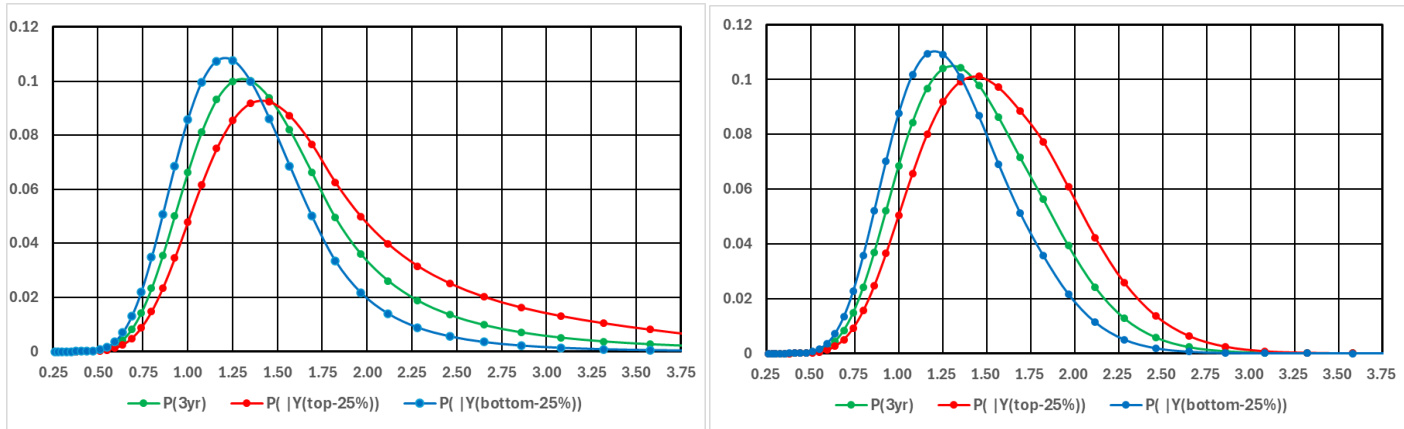
• 外部订单流影响（图9）：

引入正、负不同规模的外部订单流，显著影响价格分布尾部，外部供给增加带来价格右偏厚尾，需求增加则左偏，增强实证解释力。

2.4.2 递归效用模型数值分析（第4.2节）

• 模型特征：

无路径依赖简化设定，增量收益依赖当前价格，风险参数间固定比例\(a\zeta = \psii / \zetai\)，以此控制效用模型中续期效用重要性。

• 敏感性分析：

- 图10 价格分布随\(a\zeta\)变化，较大\(a\zeta\)增大了风险溢价，且风险溢价的时间分布特性发生变化，前期波动更显著；
- 图11 预期股价随风险参数比例变化，较大比例延伸风险溢价效应至更早时间；
- 图12 说明引入非零外部订单流后，价格分布双侧厚尾现象明显，符合理论预测。

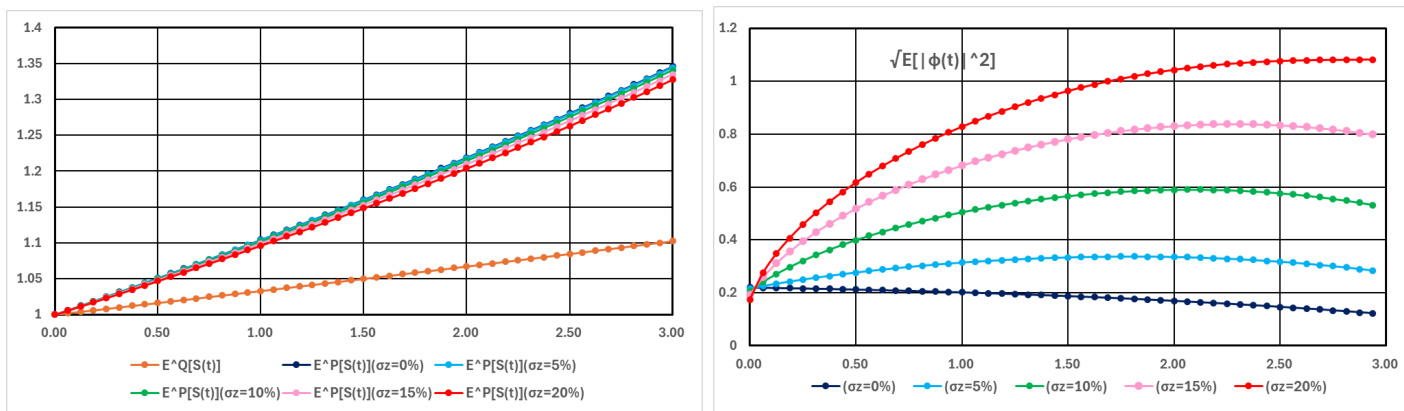
• 交易量与个体异质性波动性（图13）：

调控个体因子过程\(Zn^i\)波动率\(\sigmaz\)，发现交易量明显随其波动率增加而增大，交易活跃度与个体风险异质性强相关，而风险溢价规模对\(\sigmaz\)则表现出韧性。

---

3. 图表深度解读

以下为对报告关键图表的详细解读：

图1 (page 19)

• 内容： 展示均衡概率\(P\)和风险中性概率\(Q\)下，股票价格在第1年和第3年时的分布。

- 解读： 在1年时，均衡分布略微右移且波峰略高，显示有积极风险溢价；3年时，风险溢价效应更显著，价格右偏明显。风险中性分布对称，均衡分布因风险厌恶导致的需求不平衡而产生偏离。

• 联系文本： 与第2.4节中对负债价格敏感性的预测相符，负债与股价呈负相关推动风险溢价。

图2 (page 19)

• 内容： 3年时，根据公共因子\(Y\)的顶25%和底25%分组的条件价格分布与均衡边际分布比较。

- 解读： 顶部25% \(Y\)对应的价格分布更右偏，反映宏观利好因素下价格预期较高，而底部25%则相反，体现公共风险因子对价格的系统性影响。

图3 (page 19)

• 内容： 股票价格预期演化曲线，比较均衡概率和风险中性概率下的期望值。

- 解读： 均衡概率的期望明显高于风险中性，验证风险溢价存在且随时间递增趋势明显，合理反映风险厌恶者对额外风险的补偿需求。

图4 (page 19)

• 内容： 随时间变化的股票持仓交易量(标准差)演化曲线。

- 解读： 交易量随时间递增，反映随着市场走近终点，代理人风险管理需求加强，持仓调整更频繁，市场活跃度增加。

图5-8 (page 20)

• 内容： 负债正相关股价场景下的对偶展示（概率分布、条件分布、预期股价、交易量）。

- 解读： 价格分布向低价方向偏移，形成负风险溢价现象；预期价格下降；交易量总体更高，体现代理人冲击市场对冲的需要。

图9 (page 21)

• 内容： 引入正负外部订单流后的价格分布对比。

- 解读： 正供应导致价格右偏厚尾，正需求导致左偏厚尾，外部订单强烈影响均衡价格结构，体现均衡形成条件对市场力量的敏感性。

图10-11 (page 22)

• 内容： 递归效用模型中不同比例\(a\zeta\)下的风险溢价影响及期望股价演化。

- 解读： 高\(a\zeta\)值放大风险溢价，影响时间跨度延展，风险溢价更均匀；低值下溢价集中末期。期望股价随之升高，验证理论中续期效用的重要性影响风险偏好调整。

图12 (page 23)

• 内容： 递归效用模型下，外部订单流存在与否对价格分布的影响。

- 解读： 外部订单流出现时，分布双向厚尾，价格波动加剧，反映市场异质需求与供给力量带来的风险溢价曲线形状变化。

图13 (page 24)

• 内容： 交易量和预期股价对个体因子波动率\(\sigmaz\)的响应。

- 解读： 交易量随个体风险波动率明显上升，体现个体间不对称性驱动市场交易；相反，预期股价（风险溢价）受影响较小，显示风险溢价更依赖整体风险治理而非个体风险幅度。

---

4. 估值分析

本研究的估值不基于传统贴现现金流(DCF)，而是基于均场游戏理论框架下的均衡转移概率法，体现价格作为市场供需均衡的内生结果。该方法：

• 通过确定转移概率函数 \( p_n(\cdot) \)，保持市场清算条件，反映风险溢价和代理人异质性的宏观影响；

- 依赖代理人的效用函数（指数效用及递归效用）与风险厌恶系数分布，建立转移概率的显式表达，方便数值校准与验证；

• 估值过程为动态规划递归计算，结合二叉树递推结构化模型，降低维数灾难，提升计算效率。

从定量表现看，价格偏离风险中性测度来自于负债对价格敏感度及内部/外部风险因素的合成影响。不同效用参数及外部订单流塑造不同的风险溢价曲线，模型内部变量清楚地映射至价格估值。

---

5. 风险因素评估

报告提及的关键风险因素包括：

• 模型参数与假设限制：

影响均衡存在和唯一性的关键是效用函数形态（指数型）、指标的有界性及风险因子马尔科夫性质，假设放松或偏离可能导致均衡解不存在或非唯一。

• 市场参与者异质性变化：

个体风险偏好、负债与收益结构变化影响均衡价格和交易量，但过于同质或过于分散均可能导致模型失效。

• 外部订单流波动：

大额外部资金进出市场可引发价格显著偏离，增加市场系统性风险，可能引发均衡解多样化或临界状态。

• 路径依赖复杂性：

在递归效用路径依赖情况下，状态空间扩大、转移概率依赖历史，计算与理论分析更为复杂。

报告未明确给出缓释策略，但通过数值方法与多群体模型设计，有望在实践中增大模型鲁棒性。

---

6. 批判性视角与细微差别

• 模型依赖性强：

指数效用和递归效用虽富涵经济学意义，但对实际更复杂的非指数风险厌恶模型存在适用局限，作者也指出非指数型效用的均衡问题明显更复杂且难解。

• 路径依赖处理有限制：

路径依赖引入了非马尔科夫动态，虽然模型可扩展，但计算成本与理论难度显著提升，可能制约实际应用广泛性。

• 假设的独立同分布与市场影响力假设：

代理人为价格接受者，且个体因子间独立，忽视了市场操控、大户行为和信息关联，这在现实市场中影响强烈，可能导致模型VS现实偏差。

• 数值实验局限：

仿真仅限低维二叉树和简化公共、私有因子，参数调校较为简单，实际复杂市场的多因素、多资产情况尚待进一步拓展。

• 高效计算与多资产扩展挑战：

文末讨论均衡价格唯一性和多资产多自由度问题，强调前系统复杂度和计算瓶颈，突出模型实际部署中仍需攻克重要难点。

---

7. 结论性综合

本文开创性地将均场游戏理论与经典二叉树模型结合，为股票等资产的均衡价格形成提供数学严密且计算灵活的框架。作者针对指数型和递归指数型效用代理人，完成了均衡存在唯一性证明，并导出了显式的转移概率表达式，便于理解价格风险溢价的结构性来源：主要包括代理人的风险厌恶分布、终端负债随市场的敏感度、增量收益、及外部订单的动态变化。

数值分析具体揭示了不同因素如何塑造风险溢价曲线形态和交易量特征。以负债对股价负相关的例子，模型成功再现正风险溢价分布和价格的右偏，且引入外部订单流可以产生厚尾价格分布，解释现实市场风貌。递归效用中重要参数比例(\(\psi/\zeta\))控制风险溢价的时间结构，为解释投资者偏好时间动态提供理论支持。

此外，代理人异质性的私有因素波动是市场交易量产生的根源，为理解市场活跃度提供了机制基础。方法简单灵活，适用于多群体混合结构，较传统连续时间模型更易于计算。

展望未来，本文方法可推广至多资产、多因素模型及其他效用类型，提高模型贴合真实市场的广度和深度。结合实践金融市场的波动结构，进一步数值校准和经验验证，将促进理论成果向实际应用的转换。

---

图表Markdown引入示例

• 图1：

• 图9：

• 图13：

---

总结

本文提出的均场价格形成模型突破了传统理论在非连续交易策略和收益路径依赖上的瓶颈，系统刻画了风险溢价形成机制及市场异质性对价格交易量的驱动影响。该模型兼顾理论深度及实用数值解法，在现代金融市场复杂特征的解释与量化评估中开辟了新的方向，具有重要的理论价值和应用前景。[page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]

报告