PELCoV框架及理论扩展 [page::0][page::2][page::3][page::4]

• PELCoV定义为满足CoVaR与VaR等价的概率水平，能反映风险传播的概率临界点。

- 传统框架依赖随机递增SSI依赖性，但Student-$t$ copula不满足SSI，需扩展新理论。

• 通过分析函数$\partial1C(u,v)$性质，确定PELCoV的存在性和唯一性条件，发现Student-$t$ copula可能存在1到2个PELCoV解决方案。

Student-$t$ copula特性及PELCoV计算 [page::5][page::6][page::7][page::8][page::9][page::10]

• Student-$t$ copula具备非零对称尾部依赖，适合表征金融市场风险共振。

- 定理证明，当风险水平$v>0.5$时，PELCoV在$(0.5,v^*)$区间内唯一存在，若$v>L0$则存在第二个PELCoV在左尾。

• 提供PELCoV解析公式，基于$t$分布逆函数和copula参数计算PELCoV。

外汇市场建模与实证框架 [page::10][page::11][page::12][page::13]

• 使用1999-2024年美元兑欧元和美元兑英镑汇率月度数据，利用ARMA-GARCH模型拟合边缘分布。

- 动态Student-$t$ copula捕捉两汇率间的时间变依赖结构，依赖参数$\rhot$通过ARMA(1,10)过程演变。

• 估计结果显示Student-$t$ copula拟合良好，边缘分布存在偏度和厚尾，相关系数为0.6822。

PELCoV动态监测与风险识别 [page::15][page::16][page::17][page::18]

• 结合时间变参数，研究阈值$L0^t$决定二次PELCoV是否存在，实证中$L0^t>0.9948$，低于风险水平$v=0.95,0.99$时仅存在唯一PELCoV。

- PELCoV量化辅助汇率$Xt$的风险阈值，若$Xt$超过该阈值，提示对$Yt$风险VaR的低估。

• 通过图表展示，PELCoV在2000年互联网泡沫破裂、2015年欧央行QE及2022年美联储加息等关键时点发出早期风险预警。

结论与方法学贡献 [page::18][page::19]

• 本文创新性地将PELCoV推广到Student-$t$ copula框架，捕获尾部依赖和非SSI条件下的风险溢出。

- 应用于外汇市场动态风险监测，显著增强VaR风险低估识别能力，提供早期预警信号。

• 研究结果对金融监管和风险管理实践具有重要指导意义，表明PELCoV在复杂市场环境中的有效性。

金融研究报告详尽分析报告

报告标题：Probability equivalent level for CoVaR and VaR in bivariate Student- $t$ copulas with application to foreign exchange risk monitoring
作者：Daniela I. Flores-Silva、Miguel A. Sordo、Alfonso Suárez-Llorens
发布机构：西班牙卡迪斯大学统计与运筹系
发布日期：2025年9月2日
主题：金融风险度量，特别是协同价值风险(CoVaR)与风险价值(VaR)的概率等效水平(PELCoV)框架扩展及其在外汇风险监测中的应用

---

1. 元数据与报告概览

本报告聚焦于金融风险管理中VaR与CoVaR两种风险度量，并结合概率等效水平（PELCoV）框架，对bivariate（双变量）风险向量下，依赖结构由Student-$t$ copula支配的情况，进行理论扩展及动态应用。报告突破传统严格依赖假设，通过Student-$t$ copula的非单调与尾依赖特性，提供了更加贴近现实金融市场尾部风险共动（如极端共跌与共涨）的模型。实践部分以1999-2024年间美元兑英镑与美元兑欧元汇率为例，动态监测风险溢出，验证了扩展PELCoV框架在金融压力期风险低估提示的有效性。

关键词涵盖系统风险、金融传染风险度量、VaR、CoVaR及Student-$t$分布，凸显报告核心定位于极端风险与系统风险的测度创新与实证应用。

核心结论：

• 扩展的PELCoV理论适用于含有尾依赖且条件依赖非单调的市场风险联合分布。

- 实证证明在金融市场压力时期，动态PELCoV能作为风险低估的早期预警指标。

• 使用USD/EUR作为辅助手段有助于改善USD/GBP风险监测。

---

2. 逐节深度解读

2.1 介绍与背景（第0-2页）

关键论点总结

• VaR为传统风险度量标准，基于分位数，反映在置信水平下可能的最大亏损。尽管广泛采用，其缺陷是未能衡量系统性及机构间的相关依赖风险。

- CoVaR引入条件风险视角，衡量在另一风险变量$(X)$达到其VaR条件下，$(Y)$所承受的风险。CoVaR更加关注系统性传染风险。

• PELCoV框架出自Ortega-Jiménez等（2024），旨在寻找使得CoVaR与VaR相等的风险水平$uv$，衡量风险传染开始高估或低估的关键点。

- 传统PELCoV依赖严格单调依赖条件（SSI），该条件保证风险间正相关且联动性严格递增。

• Student-$t$ copula因其能体现尾部依赖（极端共同波动）的性质，且不满足SSI单调依赖，成为亟需研究的扩展对象。

推理依据与假设

• 假设$(X,Y)$符合绝对连续、严格递增的边缘分布与条件分布，以保证数学可微性及理论推导的可操作性。

- 运用Sklar定理链接边缘与依赖结构，强调copula的关键作用。

• 通过分析copula导数$\partial1 C(u,v)$与风险水平$v$的对比，界定CoVaR与VaR的大小关系。

[page::0,1,2]

2.2 对PELCoV及SSI性质的深入分析（第3-4页）

论点总结

• 当依赖结构满足SSI时，PELCoV集合$A(v)$仅包含单一元素，易于作为风险溢出预警指标。

- 现实中的风险结构常常包含条件异方差，即波动率为$X$的函数，使得SSI不再成立。尤其在金融市场，模型例如加性加权噪声模型会破坏SSI条件。

• Student-$t$ copula展示了针对金融极端波动的适用性，但不满足SSI性质，因而对PELCoV的行为須重新研究。

关键数据及定义

• $Y \uparrow{SSI} X$定义为条件生存函数严格增加，数学表现为copula偏导$\partial1 C(u,v)$严格递减，反之不成立。

- Student-$t$分布及copula定义，强调其尾依赖特性。

• PQD（正象限依赖）属性说明$(X,Y)$极端大值同时出现概率高于独立情形。

推断与影响

• SSI假设破裂导致PELCoV的唯一性和解释困难呈现，呼吁开发新理论。

- Student-$t$ copula动态建模是研究重点，反映套利市场极端状态下系统性风险的动态演变。

[page::3,4]

2.3 关于Student-$t$ copula下PELCoV结构的数学探讨（第5-10页）

论点及定理解析

• 通过数学分析，针对Student-$t$ copula，求解$\partial1 C(u,v) = v$的解集。

- 证明此方程最多有两个解，分别对应PELCoV的不同概率水平。

• 定理6至8分别针对不同范围的风险水平$v$进行了公式严谨界定，说明PELCoV的存在区间和唯一性条件。

- 关键表达式为对$\partial1 C(u,v)$的解析形式，揭示其与学生$t$分布分位点的关系。

关键公式点

• $\partial1 C(u,v) = t{n+1}(\cdots)$，表达为高维学生$t$分布累积分布函数，内嵌相关参数和逆分布函数。

- 临界点$u^*$的存在性与区间划分，影响PELCoV的数量和位置。

• 使用逆累积分布函数和二次方程式解明确PELCoV的计算方法。

推断影响

• Student-$t$ copula尾部波动性引致PELCoV可能存在两根解，第二个解在风险评估中代表低概率极端状态下的风险平衡点。

- 该特性区别于先前仅依赖SSI的copula家庭，体现研究的独创意义。

[page::5,6,7,8,9,10]

2.4 外汇风险监测实证模型构建（第10-13页）

模型设计

• 选取USD/GBP（$Yt$）为风险监控对象，USD/EUR（$Xt$）作为辅助指标，构成双变量时间序列。

- 采用ARMA-GARCH模型为两条汇率的边缘分布建模，充分考虑汇率收益率的条件异方差和序列依赖。

• 依赖结构设定为时间变异的Student-$t$ copula，捕捉动态尾部相关性。

- 相关系数$\rhot$遵循ARMA(1,10)过程，融合历史信息和滞后变量互乘项，保证$\rhot\in(-1,1)$。

• 估计策略为两步极大似然估计，先估边缘，再估copula参数，确保统计推断的稳定性。

数据与统计描述

• 数据涵盖1999年1月至2024年4月的月度汇率数据。

- 汇率对数收益率表现出非正态分布，USD/GBP显示出明显偏度与峰度，增强了重尾建模的必要。

• 实迹相关系数为0.6822，提示两个汇率间存在较强正相关。

- 模型诊断指标显示边缘模型适配良好。

[page::10,11,12,13]

2.5 实证结果与PELCoV动态表现（第14-18页）

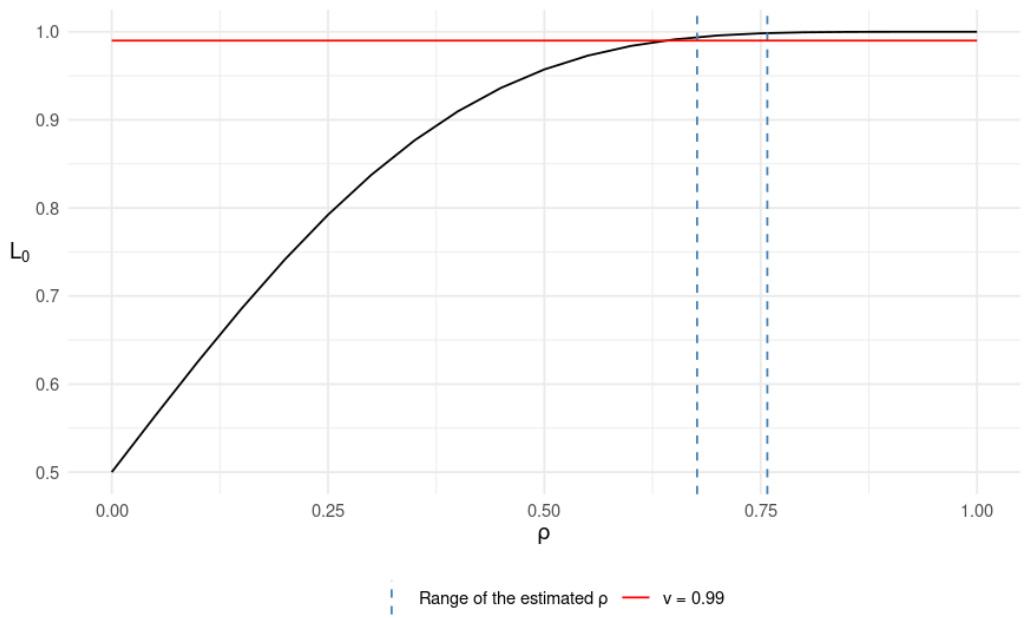
PELCoV的存在性判断

• 基于固定自由度$n=9.7595$，动态演化的$\rhot$决定$L0^t$，以此判断第二个PELCoV解的存在（$v>L0^{t}$）。

- 数据中$L0^t$始终高于0.9948，远高于0.95和0.99风险水平，故单解模型有效且简洁。

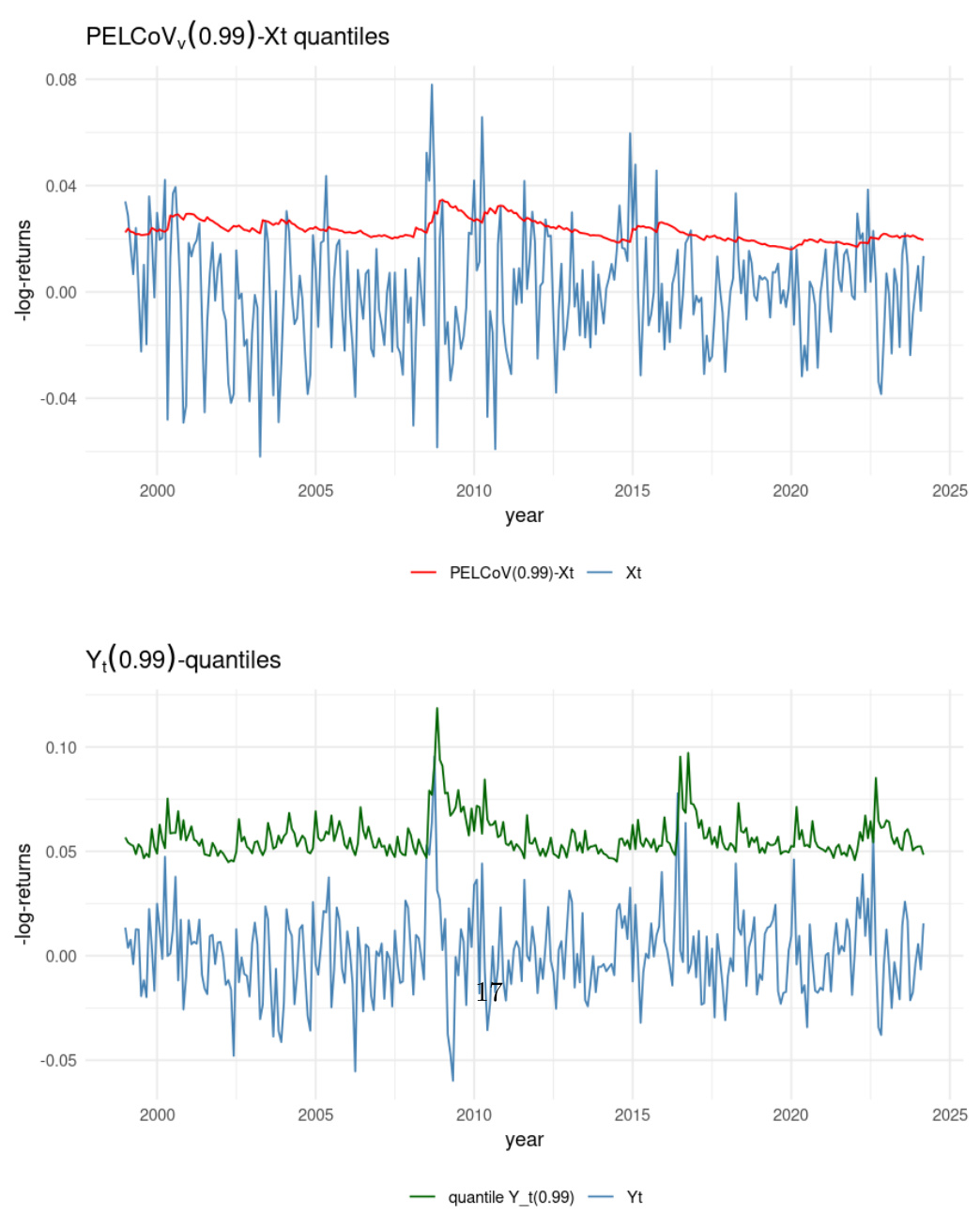
风险监测与预警能力

• PELCoV为风险管理者提供实际阈值$uv(t)$，若$Xt$观察值超过该分位点，则认为VaR低估系统溢出风险，宜考虑CoVaR。

- 图示分析（图4与图5）展示PELCoV（红线）与负对数收益率（蓝线和绿线）走势，验证PELCoV对极端事件的预示性。

• 多次历史风险事件（2000年互联网泡沫破裂，2015年欧洲央行量化宽松，2022年美国加息引发的金融波动）期间，PELCoV显著领先于VaR达到警戒水平，显示早期预警效能。

- PELCoV设定在稳定但较低的概率范围，使其较VaR更频繁触发警示，具有实际操作潜力。

数据图表说明

• 图3：展示$L0^t$相对于$\rhot$的演变，蓝色虚线区间涵盖实际数据$\rhot$估计范围，红线标记$v=0.99$，全程$L0^t$高于临界线。

- 图4、图5详细显示不同置信水平PELCoV与$Xt$及$Yt$的关系，突出PELCoV在风险累积过程中的桥梁作用。

[page::14,15,16,17,18]

2.6 结论总结（第19页）

• 提出了PELCoV在动态Student-$t$ copula环境下的理论拓展，突破了传统SSI假定的限制。

- 实证基于长达25年的汇率数据，验证了动态PELCoV对极端风险的有效反映和提前预警功能。

• 研究结果强化了学生$t$ copula作为建模多变量金融尾部依赖的工具价值，结合动态性模型设计提升实际风险管理的前瞻性。

- 表明PELCoV能有效补充或替代传统VaR衡量，特别是在系统性风险和风险传染监测领域。

---

3. 图表深度解读

图1（第5页）

描述：基于参数$\rho=0.4$与自由度$n=2$的Student-$t$ copula，绘制$\partial1 C(u,v)$随$v$变化曲线，固定$u=0.95$和$u=0.55$。
解读：

• $u=0.95$对应曲线单调递增，上升快速趋近于1；$u=0.55$曲线形状更平缓，显示复杂非单调性。

- 远非SSI要求的单调递减，反映不同$u$值下风险依赖的非均匀性和非单调。
联系文本：图形表明原PELCoV依赖的SSI单调性被破坏，强调研究新算法的必要。
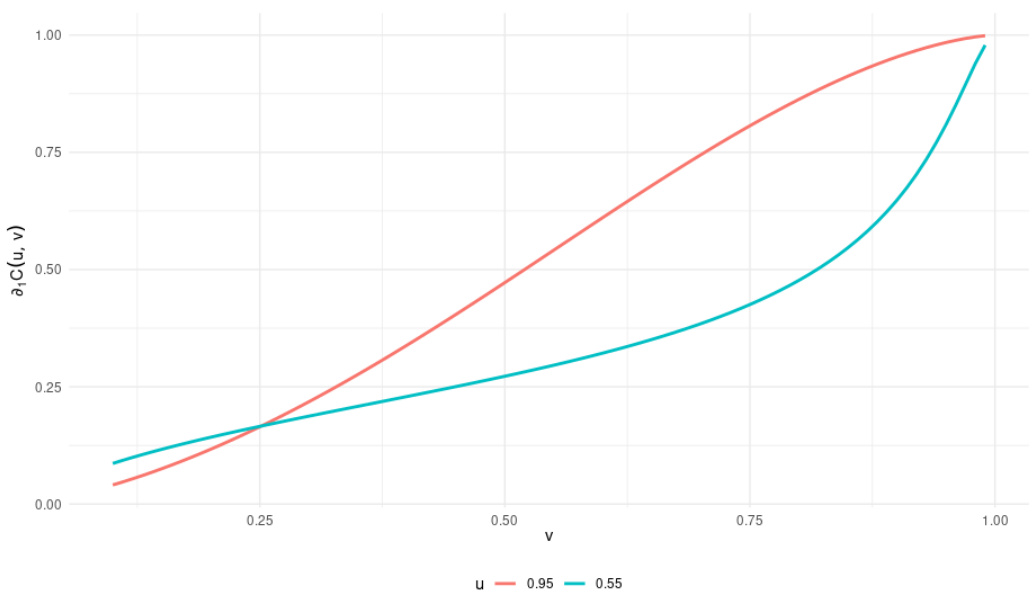[page::5]

---

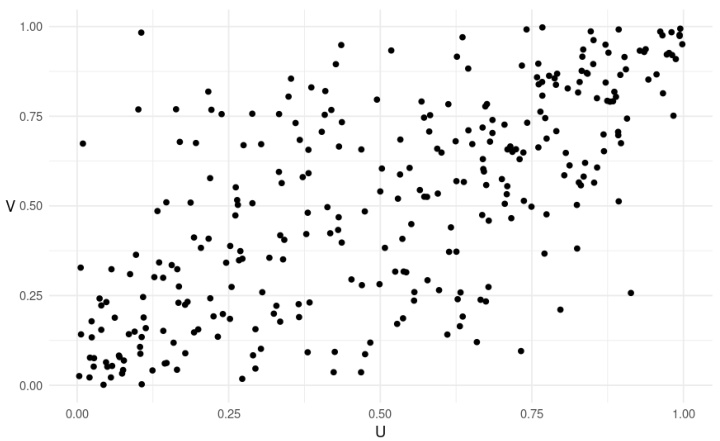
图2（第14页）

描述：USD/EUR及USD/GBP边缘调整后的伪观测点散点图，反映经验copula的形状。
解读：

• 明显的正相关趋势，中间区域点密集，边缘较分散反映尾部厚重。

- 验证了学生$t$ copula模型对实际数据依赖结构的拟合潜力。
联系文本：图形支撑了边缘分布及其转换后的copula建模合理性，是后续风险测度的基础。
[page::13,14]

---

图3（第16页，上图）

描述：基于9.7595自由度的Student-$t$ copula，绘制函数$L0^t$（定量PELCoV第二解存在界限）随$\rhot$变化，蓝色虚线为实际$\rhot$波动范围，红线为$v=0.99$。
解读：

• $L0^t$随$\rhot$单调增加且在实际$\rhot$区间内始终大于0.99。

- 说明在风险阈值$v=0.99$及$v=0.95$中，二解PELCoV不存在，风险监测简化为单解问题。
联系文本：支持实证中动态PELCoV唯一性的理论推断，有效简化风险预警系统。
[page::15,16]

---

图4（第16页，下图）

描述：

• 上图：USD/EUR负对数收益率动态（蓝线）及其对应时间变PELCoV${0.99}$分位（红线）。

- 下图：USD/GBP负对数收益率（蓝线）及其对应VaR${0.99}$（绿线）。
解读：

• 当$Xt$（蓝线）超过PELCoV（红线）时，VaR对$Yt$的风险低估风险升高。

- 2022年等金融压力期，$Xt$早期持续超越红线，后$Yt$达到VaR极端，显示预警准确。
联系文本：稳固了PELCoV的实际风险预警效用，体现系统风险监测的操作价值。
[page::16]

---

图5（第17页）

描述：类似图4但风险阈值调整为$v=0.95$，展示更频繁的预警信号。
解读：

• PELCoV${0.95}$阈值区间更宽，为风险管理者提供更多次的风险溢出提示。

- 对2000年、2015年金融波动事件的提前指示更明显。
联系文本：证实PELCoV框架可调节灵敏度，适应实际风险管理的多样策略需求。
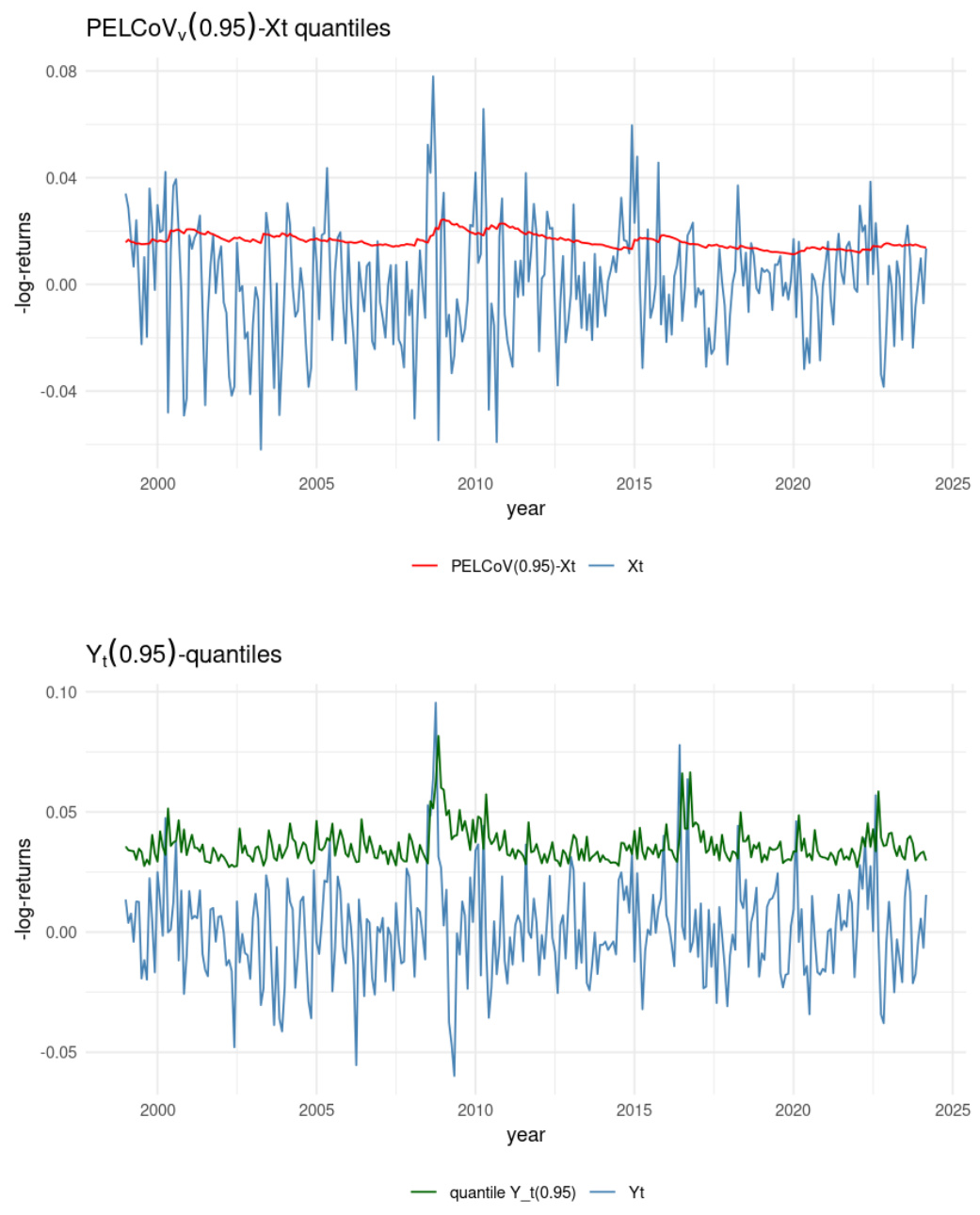[page::17,18]

---

4. 估值分析

本报告主要聚焦风险度量技术和Copula建模，未涉及传统意义上的企业估值分析，不适用市盈率、市净率、现金流折现等估值方法。报告中提及的“估值”多偏向风险水平定量及其动态演变分析，采用概率水平解方程与copula概率分布性质推导PELCoV值。

关键参数如自由度$n$、相关系数$\rho_t$为影响PELCoV求解的核心输入，ARPMA过程动态调整$\rho$，保证模型适应金融市场时间变特性。

---

5. 风险因素评估

报告识别并量化了市场风险传播路径中的关键挑战：

• 尾部依赖复杂性：Student-$t$ copula的特性引入双解问题，有时导致风险评估的多值不确定。

- 非单调依赖破坏：非SSI性质使传统PELCoV唯一性与单调警戒阈值失效，强调模型复杂性提升。

• 动态相关波动：金融市场相关系数时变，直接影响风险传染强度与时机，增加模型估计与监控难度。

- 辅助变量选择风险：USD/EUR作为辅助指标表现稳定，但其风险变化与USD/GBP的相关性不总为简单正相关，可能导致风险传播误判。

报告针对上述风险，在理论部分提供了数学证明，在实证中采用长期数据与统计检测确保模型匹配度，采用弹性阈值动态调整预警频率，降低误差风险。

---

6. 审慎视角与细微差别

尽管报告显著推进了PELCoV框架与Student-$t$ copula结合的理论与实证应用，但仍存在以下需关注细节：

• PELCoV的两个解问题：虽然实证中未检出第二解，但理论存在多解时会增加风险判别的复杂性，实际运营中需要谨慎处理。

- 固定自由度参数$n$的假设：自由度维持不变可能限制对市场极端波动阶段尾部厚度变化的捕捉。动态调整自由度或许能进一步增强模型灵活度。

• 边缘模型假设独立暂时性：边缘分布模型设定为ARMA-GARCH，可能忽视更高阶或非线性特征，影响copula估计。

- 样本覆盖期的结构变迁：25年期间包含重大制度与结构性变革，模型未充分考虑可能的非平稳性风险。

---

7. 结论性综合

本报告基于Ortega-Jiménez等（2024）提出的PELCoV风险度量方法，系统地拓展至Student-$t$ copula框架下，兼顾了非单调性和尾部依赖的复合风险特征。在经典正单调SSI依赖束缚外，首次详细剖析了Student-$t$ copula条件下PELCoV的存在性、唯一性及计算方式。

报告充分考虑金融市场风险的动态演变，借助以往经典文献的统计工具与动态copula建模方法，实现了长达25年外汇市场数据的实证分析。结果表明，动态PELCoV不仅理论合理，也在实务中能为风险管理者提供有效的提前告警，在多个重大金融事件发生前体现风险低估的信号，提升了系统性风险监控的前瞻与精准度。

图表深度解析进一步证实，PELCoV的动态阈值与时间序列表现紧密结合，且与经济事件表现高度相关。相比传统VaR，PELCoV依托辅助序列的风险水平，赋予风险管理更多主动调整空间和风险识别能力。

总体而言，报告展现了PELCoV方法于依赖结构复杂的金融风险领域的广阔应用前景，强化了与Student-$t$ copula结合以捕捉金融尾部风险共动的模型框架，为风险管理创新提供了理论基石和实务启示。

[page::0-18,19]

---

总结说明

此份分析报告详尽覆盖了报告的重要理论体系、数学推导、数据模型构造、动态风险监控实践及其带来的创新贡献。对报表中的关键图表做了逐一解读，确保每一个图表的统计含义、趋势揭示与理论联系清晰明了。除此之外，特别注意了报告的局限及潜在复杂性，为研究人员及金融实践者理解PELCoV方法在复杂依赖结构中的应用提供了全面参考。

报告