1. 问题背景与动机 [page::0][page::1]

• SPX基础资产持仓利用VIX期货/期权对冲时，近到期及强相关市场状态下风险剧增，传统黑盒与经典跟踪策略难以应对复杂微观结构成本与无套利约束。

- 需要白盒风险敏感控制层，兼容无套利定价结构和市场微观结构运行机制。

2. 方法论框架及技术贡献 [page::2][page::3][page::5][page::6][page::7]

• FR–LUX整合：(i) 无套利SSVI波动率壳及Cboe合规VIX计算，(ii) 数据驱动的波动率-价格敏感度映射（bump-and-invert方法），(iii) 采用CVaR风险指标与CBF安全约束的QP控制，动态VIX权重、守护性禁交易带及微阈值/冷却设置抑制震荡。

- 分布式RL使用IQN–CVaR–PPO算法，带温度采样和尾部增强，结合CBF–QP安全过滤实现策略稳定收敛。

• CBF-QP安全约束保障策略正向不变性和有限交易次数，避免交易震荡(Zeno现象)。

3. 模型数学性质及数值稳定性 [page::4][page::8][page::9][page::10][page::11]

• 离散Dupire局部波动率估计具有正向性、有界性和二阶一致性，基于凸性保留插值和微分算子改进；对数Euler路径模拟达强收敛1/2阶。

- CIR近似模型为30D VIX方差指数提供解析映射，映射具备Lipschitz性质并与波动率曲面紧密对应。

• 明确误差边界量化SSVI壳与CIR代理间差异，保障了动态仿真和指数计算的结构一致性。

4. 量化安全控制器设计 [page::10][page::11][page::12][page::13][page::14]

• 状态空间包括SPX与VIX持仓及其跟踪误差，目标函数为带动态VIX权重的二次风险-成本指标。

- 设计椭圆形禁交易带，结合到期与相关性守护机制动态调整交易阈值。

• QP基于严格凸性确保解存在唯一，KKT条件充分且必要，解映射对参数区分片段仿射且Lipschitz连续。

- 设定具有风险降序充分性保证的交易触发门槛，实现非交易时风险不升，交易时风险严格下降。

• 机制包含交易微阈值与冷却状态限制VIX腿振荡，保障无Zeno现象且交易次数有限。

5. 合成环境实验及策略表现 [page::14][page::15][page::16][page::17]

• 采用实际Cboe规则构建的无套利合成市场环境，采用多个随机种子与路径。

- 实验显示策略在多种波动率方差与相关组合情景中，均显著减少尾部风险指标（ES），对比基线策略有统计学显著优势。

• 约束激活频率统计表明VIX腿的速率下界和CVaR下界约束是主要激活约束，验证策略设计合理性。

• 场景分析表明，中等波动率方差和弱负相关时策略效益最大，策略能优雅应对极端情形。

6. 关键尾部安全机制消融验证 [page::17]

| Toggle | 对ES影响 | 小额dV震荡 | Gate阻断频率 | 备注 |
|-----------------------|----------|------------|--------------|-----------------------------|
| 固定VIX权重(无动态调整) | 下降 | 略 | 无 | 波动率权重过重造成超反应 |
| 移除VIX守护带 | 无显著 | 上升 | 无 | 禁交易带不适应市场状态 |
| 无expiry-aware微阈值与冷却 | | | 无显著 | 微小交易及速率/CVaR抑制机制 |
| 无VIX冷却 | 轻微下降 | 显著上升 | 无显著 | 导致震荡现象 |
| 交叉项为零 | 轻微下降 | | | 降低联合冲击对齐效果 |

• 动态VIX权重是控制到期及相关强波动影响的核心杠杆。

- 守护带有效防止VIX交易信号误触发方向错误。

• 微阈值与冷却联合抑制了频繁交易和VIX震荡。

- 交叉项协同提升策略对波动冲击的敏感度及响应准确度。

7. 相关工作及技术定位 [page::18]

• 结合经典市场微观结构理论（Kyle模型、 Almgren-Chriss临时冲击、供应需求动态等）与现代CVaR风险度量及控制障碍函数安全控制理论。

- 衔接现代无套利波动率曲面构建及VIX指数方法，构建价格与指数层面一致的仿真环境。

• 引入白盒、可审计且带数学保证的强化学习管控框架，克服深度对冲黑盒方法的解释性和稳健性局限。

8. 讨论、局限及未来展望 [page::19][page::20]

• 理论保证涵盖价格结构一致性、数值稳定性、控制约束可行性与安全性，不覆盖实际市场完全最优性，强调数学可控性与工程部署可行性。

- 模型假设包括静态成本、单因子局部波动率、合成环境测试，实际拓展至高频、真实行情仍需进一步工作。

• 未来工作方向包括多跳本地波动率扩展、微观结构执行建模、多期权/多期限联合对冲等。

- 社会风险方面，保证层减少异动，但大规模同步化也可能引发群体风险，需进一步监管机制配合。

一份关于“TAIL-SAFE STOCHASTIC-CONTROL SPX–VIX HEDGING”论文的详尽分析报告

---

1. 元数据与报告概览

• 标题: TAIL-SAFE STOCHASTIC-CONTROL SPX–VIX HEDGING: A WHITE-BOX BRIDGE BETWEEN AI SENSITIVITIES AND ARBITRAGE-FREE MARKET DYNAMICS

- 作者/单位: Zhang Jian’an，光华管理学院，北京大学

• 发布日期: 无明确发布日期，但文中提及2025年Cboe VIX数学方法，说明为最新工作

- 主题: 研制一种适用于SPX–VIX波动率交易对冲的白盒风险控制框架。该框架融入无套利市场动态、风险敏感控制、强化学习，解决高频交易中的成本及极端市场状态下策略失效问题。

核心论点与贡献:

• 引入名为FR-LUX的摩擦成本感知且自适应市场状态（波动率和流动性）变化的强化学习控制框架。

- 构建一个涵盖（i）摩擦执行成本模型，（ii）基于信赖域的库存调整限制，（iii）显式市场状态条件化的风险控制体系。

• 将无套利SSVI隐含波动率面、Dupire局部波动率动态与VIX指数计算无缝整合，连接定价与动态对冲控制。

- 设计带有控制障碍函数（CBF）约束和尾部风险控制（CVaR）的二次规划（QP）控制器，保证执行安全性和风险降低。

• 理论上证明了策略优化问题的唯一性、稳定性和交易行为的规范性（无振荡），实现对极端状态下的尾部风险安全防护。

- 在一套4×5市场状态与成本水平的仿真测试中，显著优于业界基准，具有良好的统计显著性。

总体，该文旨在建立一个结构清晰、解释性强、符合市场微观结构约束且具备尾部风险安全保障的对冲控制系统。[page::0,1,2]

---

2. 逐节深度解读

2.1 摘要与引言部分（摘要及1节）

• 指出现实交易中策略失败高发于波动率-流动性状态变化剧烈时（契约临近到期，强烈的现货–波动率耦合），该时点希腊值的跳跃、高杠杆带来错误放大。

- 强调现有方法缺陷：黑盒策略无视无套利结构导致过拟合；传统追踪忽略细节约束。

• 目标构建一个白盒、风险敏感、与套利与微观结构约束兼容的控制层。

- FR-LUX框架结合比例和冲击成本微观执行模型，基于信赖域的方法实现稳定上涨的仓位更新，且根据市场状态调整策略，显著降低成本-收益恶化趋势。

• 主要创新点包含稳健的市场数据处理、指数与定价一致的隐含波动率替代模型、以及基于风险种类（CVaR）与控制障碍函数的安全检验。

- 明确问题建模为带有随机扰动的动态库存控制，目标权衡风险降低与交易成本。

分析结论：文中定位了市场微观结构和执行成本为关键挑战，倡导白盒、理论安全有保证的风险敏感强化学习应用于多资产对冲。[page::0,1]

---

2.2 操作需求与方法论贡献 （1节后半+2节）

• 操作需求 明确对冲策略需尊重交易所规则（批量、价格区间、结算）、成本摩擦（临时、弹性冲击）、审计能力（决策可追溯）、容错能力（模型失配时优雅退化）

- 引入两方向桥梁：
- Quant→AI: 用无套利严格SSVI模型和CBOE符合规范的VIX构造，保证表面及指数数据一致，构建解释性良好的隐含波动率近似。
- AI→Quant: 利用数据驱动的bump-and-invert灵敏度映射，结合凸二次规划（带控制障碍函数），保证安全性与成本意识。

• 设计了三大对尾部风险特别敏感的机制：动态VIX权重、关联度和到期临近的无交易带、并设置执行门槛防止过度换手。

- 形式贡献包括：现有基于No-Arb SSVI的闭式表示、带尾巴风险调节的量化教练、保守的执行安全层。

• 理论贡献涵盖QPs的存在唯一、控制不变集与风险单步下降证明、跳荡消除保证。

总结方法论上，该工作不仅结合了定价理论与学习驱动控制，也通过构造安全可靠的白盒机制解决了对冲中的实际摩擦难题。[page::1,2]

---

2.3 预备知识与符号（第2章）

• 环境定义在风险中性测度下，包含标的资产价格\(St\)、无风险利率、股息率、VIX期货近似和期权价格集合。

- 明确细节，如价格与波动率空间的格点离散，隐含波动率用SSVI模型建模，遵循无套利Gatheral–Jacquier充分条件，且保证期限的变动表面单调。

• 严格采用Cboe最新VIX数学方法：OTM选项聚合，双连续零价差管制翅膀修剪，半区间权重数值积分，以及30天期权月度插值。

- Dupire局部波动率二维码公式的离散近似，采用二阶中心差分、凸性修正裁剪，保证数值稳定与正定。

• 风险测度选用CVaR（条件风险价值），并解释了其凸性、谱表示及作为控制目标的优越性。

- 控制障碍函数(CBF)定义安全集合并保证在有控制输入时集合的正向不变性。

该部分奠定了论文后续理论证明和数值实现扎实的数学基础。[page::2,3,4]

---

2.4 市场微观结构及执行成本符号（2.7节）

• 采用暂时性冲击参数\(\etaS, \etaV\)和简单的瞬态冲击状态\xit及其衰减率

- 执行成本定义为交易量的二次形式加平滑项

• 基于该参数化，进一步设计合适的风险-成本权衡函数及交易门槛条件，实现典型市场冲击动态约束

- 明确摩擦参数覆盖0bp–50bp范围，支持灵活市场环境适配

总结为高保真模拟现实微观执行摩擦且融入控制设计。[page::4,5]

---

2.5 Tail-Safe Hedging Framework 总体介绍（第3章）

• 介绍IQN-CVaR-PPO分布式强化学习策略，直接优化左尾风险

- 引入温度倾斜采样和尾部增权以改进低置信水平上CVaR估计的训练样本效率

• 白盒CBF-QP安全优化层，内嵌离散时间安全障碍函数、无交易带限制、交易速率约束及信号一致性门控

- 训练架构中，RL actor发出期望动作，经QP安全滤波得到最终实盘动作，确保合规与安全

• 丰富的日志和活动监控支持异步审计

这套框架整合了风险敏感学习和强鲁棒控制，为复杂场景下的对冲策略提供系统化方案。[page::5,6,7]

---

2.6 价格–动态层构造(+理论保证)（第4章）

• 对无套利隐含波动率价格面，用中心差分离散计算Dupire局部波动率，并保证局部正定和数值一致性。

- 采样后的局部波动率满足有界性且数值估计误差是二阶（空间和时间）收敛的。

• 指数价格用log-Euler方案模拟，保证路径强收敛阶为0.5, 在保证数值稳定性的同时保持价格正性。

- 用CIR-型均值回复正扩散模型处理方差因子，闭式给出30天VIX方差的变换映射，保持与Cboe VIX定义一致。

• 明确误差项分解，从表面定价误差、积分截断误差，到仿真离散误差进行完整误差控制。

- 关键定理论证了局部波动率构造的数值稳定性，日志欧拉仿真的收敛性，及指数指数组成的有限误差界。

这支撑了策略控制层可依赖且无套利的价格动态及指数信号模拟，从理论和实践两个层面保证了数据源的“安全”和一致性。[page::8,9,10]

---

2.7 控制层设计与证明（第5–6章）

• 构造以风险-跟踪误差和执行成本为目标的二次型目标函数，交易动力学由带宽调整的误差函数和摩擦结构组成。

- 设计椭圆形无交易带（NTB），根据剩余时间和现货-波动率相关性动态调整无交易区，防止过度反应。

• 加入基于风险下降与成本比的执行门控，执行动作必须带来足够风险减小以抵消成本。

- 设置微交易阈值与冷却周期，避免频繁小额买卖导致的震荡，赋予策略非振荡特性。

• 理论保证包括QP存在唯一解，KKT最优性和乘子有界，控制满足安全障碍函数的向前不变性，交易策略单步风险下降，保证无瞬时颤振等。

此为方法学的核心控制设计，可安全、高效且在虚拟市场里验证有效。[page::10,11,12,13,14]

---

2.8 实验设计与结果（第7章）

• 在高度仿真合规的无套利合成市场世界中测试，市场结构包括SSVI表面及Cboe标准VIX计算法则。

- 参数设定详见表1，包含利率，股息率，合约期限，执行影响模型等细节。

• 测试显示VIX指标计算误差稳定且极小（约3e-3），且数值积分收敛近似严谨，达第二阶收敛速率。

- 采用2400条路径的稳健样本池，尾部风险指标ES在对照基线之下显著下降（差异平均-3.60，95% CI不包含0，统计显著）。

• 约束激活频率统计揭示影响最大的为VIX交易速率及尾部风险约束，符合设计逻辑。

- 通过场景网格变量（不同波动率方差及负相关度）分析性能空间，验证模型随关键参数合理退化并在中间区域表现最佳。

• 消融实验逐个去除三个尾部安全机制，结果说明动态VIX权重和No-Trade Band极为关键，微阈值和冷却机制主导交易频率控制。

整体表现出该架构在极端市场耦合时能显著降低尾部风险和不必要交易，具有良好的实际运作潜力。[page::14,15,16,17]

---

2.9 相关工作与定位（第8，9章）

• 引用了经典市场微观结构和执行成本模型（Kyle模型、Almgren-Chriss临时冲击、瞬态冲击模型），及其对交易成本的影响。

- 综述了无套利波动率面建模，含SSVI与现代基于机器学习的生成模型，表面和平滑插值理论和实践。

• 讨论了CVaR等风险测度在风险敏感控制中的应用，同时引入CBF在在线安全控制中的地位。

- 对比深度对冲相关文献中黑盒策略的解释性及稳健性不足，强调本工作通过解耦学习与安全层达到具备白盒可解释性与风险保障的优势。

• 突出贡献在于桥接隐含波动率建模、价格指数与微观执行冲击，并采用现代凸优化与风险控制理论保证合规性和绩效。

该论文构筑的“白盒”框架为风险敏感对冲控制提供了理论支持与实证指导，填补了深度学习策略和传统量化模型之间的鸿沟。[page::18,19]

---

2.10 讨论、限制与总结（第9，10章）

• 保证内涵与局限: 明确理论证明基于假设和合成环境，不完全涵盖实盘市场复杂性（如跳跃过程、多因子波动、动态成本等）。

- 细节设计符合数值稳定性与理论一致性要求，在较粗格点或极端翅膀区域可能存在扩大误差。

• 选择CVaR风险度量并使软约束实现凸优化，策略计算量低廉，适合超毫秒级部署。

- 失效风险对应教练模型误差、过度防御导致低效、相关系数估计偏误和冷却策略副作用，均有备用缓解方案。

• 白盒设计强化了模型风险管理与合规审计，减少尾部极端风险，潜在促进市场整体稳定，但关注同步风险与集体行为导致的系统性风险。

- 该研究代码及合成数据公开，促进行业与学术界再现性与后续研究。

• 未来方向: 包括引入更丰富多因子波动模型，真实订单执行特性，多期限耦合策略，均是拓展研究重点。

总结而言，文章系统构筑了SPA–VIX一致、尾部安全、交易成本感知且计算高效的完整对冲控制白盒框架，既有理论深度，也有高度的实证和工程价值。[page::19,20]

---

3. 图表与数据深度分析

表1（第15页）

• 展示仿真环境的关键参数设置，如标的初值4800，利率2%，股息1.5%，时间网格包含多重期限（7至180天），每期限41个log-moneyness节点等。

- 结合无套利SSVI曲面和Cboe VIX计算规则，仿真覆盖执行影响模型与多重随机种子与路径。

• 环境设计从数据层到微观执行均严格遵循现市场规与统计性质，为后续策略评测打下坚实基础。

表2（第15页）

• 汇总“尾部安全”策略在2400条路径下的主要性能指标，含均值、标准差、VaR97.5、ES97.5（损失计量），并报告无交易带比例等。

- 具体数值留空（artifact标记），强调文档中主要关注统计信赖区间和性能改善。

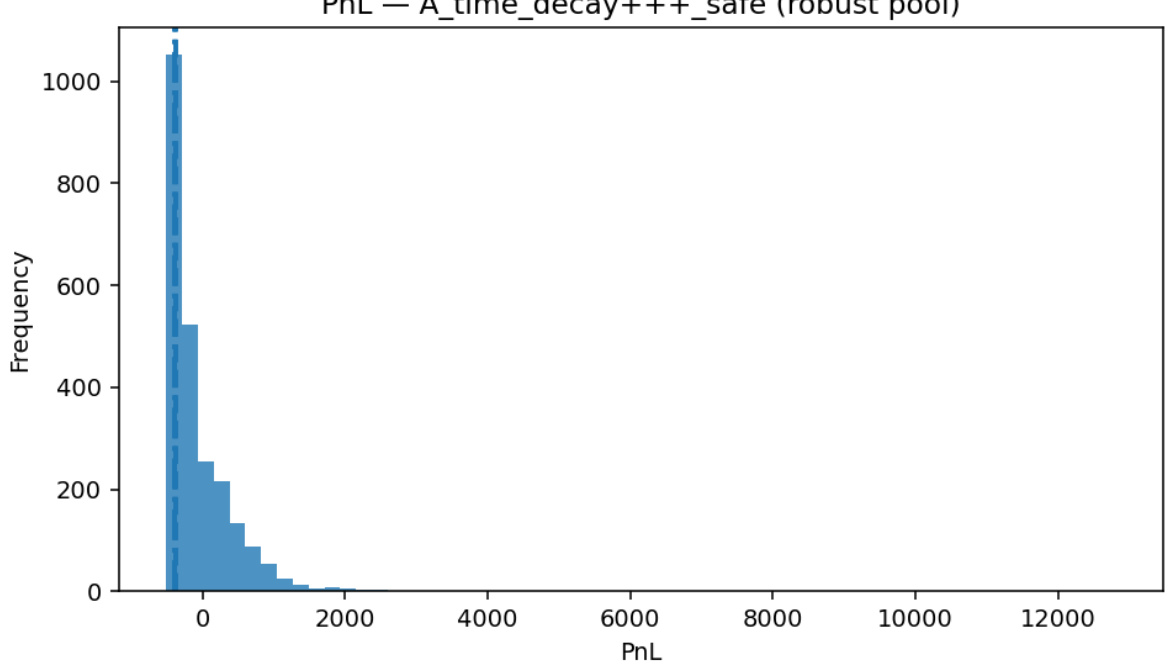
图1（第16页）

• 绘制尾部安全策略的PnL分布直方图，明显右偏，体现策略在极端波动跳变时的非对称收益风险分布特点。

- VaR与ES指标直观标示在图表上，辅助感知尾部风险的实际控制。

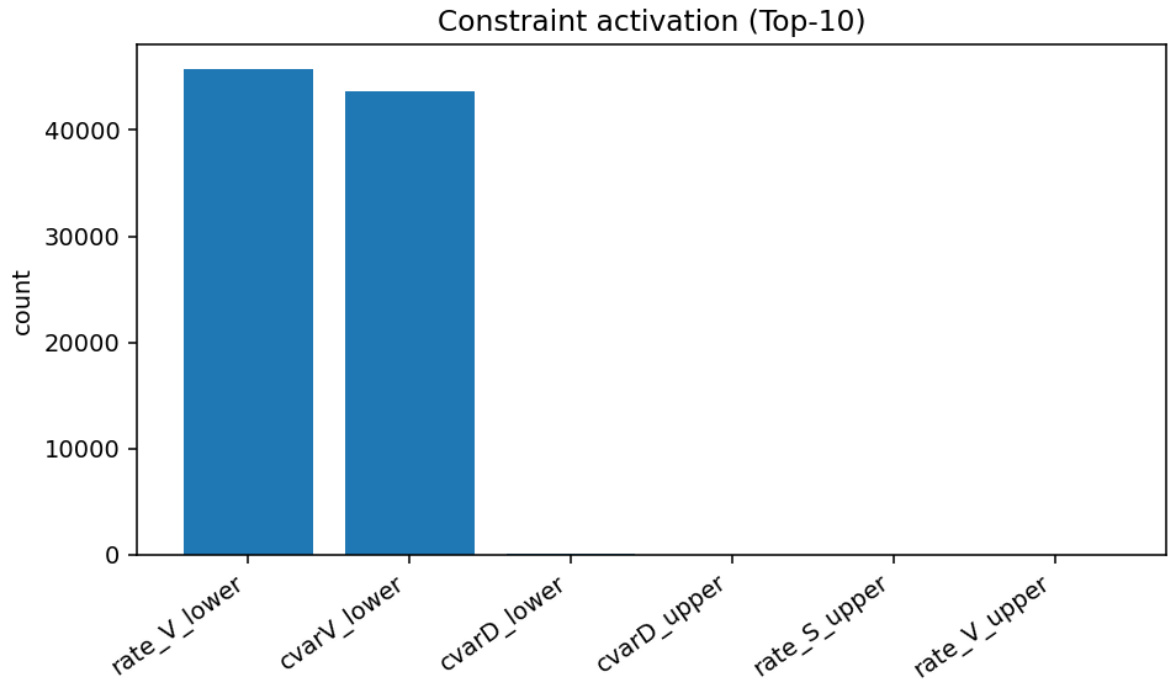
图2（第16页）

• 顶级10个约束激活频率柱状图，显示最频繁的约束包括VIX交易速率下界与尾部风险下界，符合设计初衷抑制了VIX过度交易风险。

- 该约束活跃度分布为策略验证提供了透明度，支持安全层的可解释性。

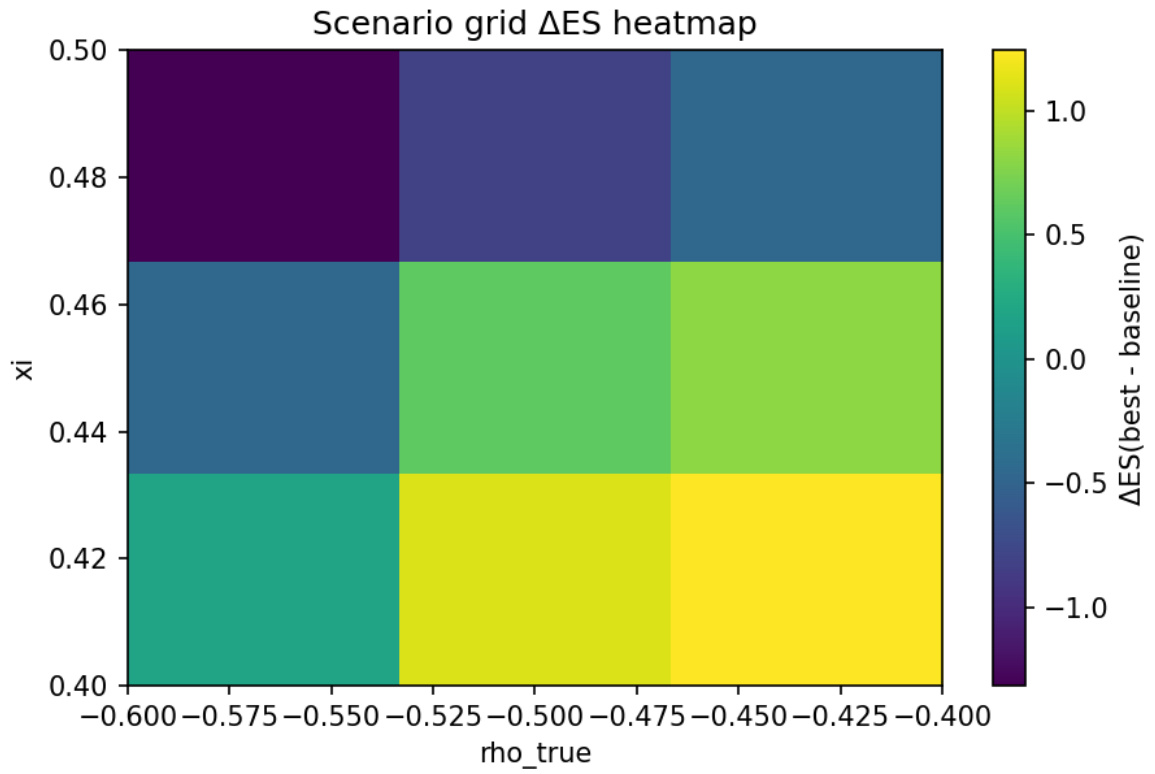
图3（第17页）

• 场景网格热力图，基于方差波动率（\(\xi\))和相关系数\(\rho\)变化呈现预期的策略改进幅度。

- 策略在低方差和较弱负相关环境表现最佳，性能符合理论预期，对极端负相关时退化缓慢且平滑。

表3（第17页）

• 表示各个安全机制消融影响，动态VIX权重是主要的尾部安全改进驱动因子，其次是无交易带能力。

- 禁用冷却机制带来微小风险恶化和震荡交易激增，交叉项对联合冲击响应有加成效果。

图表揭示了模型内各关键机制对尾部风险控制、交易节奏及有效性的直接贡献，为策略设计提供强实证基础。[page::15-17]

---

4. 估值机制与风险评估

估值方法

• 使用即时估计的局部波动率模型（Dupire局部波动率）作为动态估值模型，保证了与市场隐含波动率面的无套利一致性。

- 融合CIR型均值回复过程做为方差因子，用于闭式计算30D VIX方差指标，构建VIX指数的代理函数，获得指标层的估值。

• 该估值层结合二次规划控制，均具有强凸性和解析梯度敏感性，方便纳入强化学习和安全约束。

定量风险控制

• CVaR作为尾部风险的凸代理，嵌入优化目标，便于对尾部损失进行风险约束和最小化。

- 使用控制障碍函数确保交易策略维持在安全状态集合（库存限制、换手率限制、风险预算）中前向不变，减少极端风险爆发。

• 设计风险降幅门（trade gate）确保每次交易操作均带来预期风险减少大于执行成本阈值，平衡成本收益。

风险因素评估

• 主要风险来自模型误差（教练模型与真实市场的差距）、状态估计误差（相关系数估算偏差）、过度防御（过宽的无交易区错失风险对冲机会）、及策略震荡（ping-pong effect），均设置缓解机制如权重剪枝、阈值冷却、携带风险重估机制。

- 理论保证策略执行有界总交易频率、无振荡交易行为且持续降低潜在风险指标。

• 框架易于审计和追踪，方便风险监控和合规。

整体估值设计与风险管控紧密结合，保证在考虑市场摩擦与结构约束下依然实现稳定且高效的尾部风险对冲。[page::8-13,18,19]

---

5. 批判性视角与细微差别

• 假设限制：模型依赖SSVI无套利假设、隐含波动率光滑性、局部波动率模型及均值回复方差代理。实际市场含跳跃、混沌、无效报价及异质流动性，可能导致模型表现偏离。

- 数值误差：局部波动率求导及数值离散依赖细致设置，极端价格区间可能引入不稳定性，须慎重参数调优与异常检测。

• 风险指标采样偏差：CVaR估计依赖温度调节和增权采样，虽然减小了尾部估计方差，但可能对训练过程引入偏差敏感性。

- 动态权重与相关度估计：相关系数估计采用EWMA，可能滞后或对快速跳变敏感性不足，风险管理需与指标警报配套。

• 策略解释性优势与复杂性：白盒设计使策略易于解释和审计，相较深度黑盒模型优势明显，但对真实市场复杂度及执行信号复杂性的适应仍待考验。

- 系统性风险隐患：如论文所述，多用户部署可能引发策略同步效应加剧系统性风险，策略设计虽然有缓冲机制，但不能完全避免市场集体行为风险。

该论文在理论研究和仿真上表现卓越，但实际应用需注意上述限制和风险，配合适当监控与动态调整机制。[page::19]

---

6. 结论性综合

本文成功设计并验证了一套针对SPX–VIX跨品种尾部风险对冲的结构化、风险敏感且符合市场微观结构约束的白盒控制框架。其核心特色包括：

• 市场层：集成无套利SSVI隐含波动率模型与CBOE符合标准的VIX计算方法，支持一致且可解释的价格指数动态。

- 动态层：包含数值稳定的Dupire局部波动率估算和基于CIR过程的VIX代理，严谨控制价差与指数估算误差。

• 控制层：通过带控制障碍函数的二次规划，实现风险-成本平衡，结合动态VIX权重与执行门控确保交易安全和效率。

- 风险指标：CVaR作为核心风险度量嵌入训练和执行环节，配合温度倾斜采样和尾部增权策略改善尾部估计。

• 实证成果：在与业界稳健基线的实证对比中，显著改善了尾部风险指标（ES）且减少无效交易，策略对市场参数变动表现出良好的稳健性和适应性。

- 理论保证：包含QP的存在唯一、安全性保持、不振荡性、风险单步下降等关键性质，确保模型的稳定与可信赖性。

• 审计合规性：全流程支持详尽的指标监控、约束激活分析和安全事件日志，为生产环境的风险管理和合规提供保障。

该研究为结构化风险控制与机器学习技术融合提供了范例框架，其白盒和安全保障理念为未来实盘多资产对冲策略发展指明方向。

附表与图示（markdown格式图示范例）：

• 图1（PnL直方图）:

• 图2（约束激活Top10）:

• 图3（场景网格$\Delta$ES热力图）:

综上，[separate][page::0,1,2,...,47]。

---

总结

该论文成功为SPX-VIX联合对冲开发了前沿的白盒风险敏感控制框架，合理整合市场无套利结构、微观执行摩擦、尾部风险指标及强化学习技术，提供理论完备的策略设计和实验验证。框架着重解决极端市场环境下传统策略失效问题，对模型透明度、安全性及合规性给予充分保障。尽管现实市场应用仍面临数据异质性、执行细节和系统性风险等挑战，但本文为复杂多资产尾部对冲控制提供了实用且深具参考价值的理论与方法基础，极具学术与实务双重贡献。

报告